Question

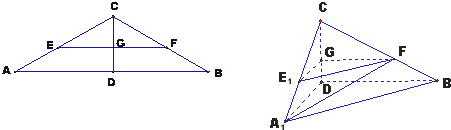
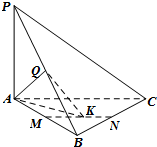
如图，在三棱锥P-ABC中，直线PA⊥平面ABC，且∠ABC=90°，又点Q，M，N分别是线段PB，AB，BC的中点，且点K是线段MN上的动点．
（Ⅰ）证明：直线QK∥平面PAC；
（Ⅱ）若PA=AB=BC=8，且二面角Q-AK-M的平面角的余弦值为

3

9

，试求MK的长度．

Answer 1

（Ⅰ）连结QM，∵点Q，M，N分别是线段PB，AB，BC的中点
∴QM∥PA且MN∥AC，从而QM∥平面PAC且MN∥平面PAC
又∵MN∩QM=M，∴平面QMN∥平面PAC而QK?平面QMN
∴QK∥平面PAC…（7分）
（Ⅱ）方法1：过M作MH⊥AK于H，连QH，则∠QHM即为二面角Q-AK-M的平面
角，设MK=x，且PA=PB=PC=8则MH=

2 2 x

x2+4 2 x+16

，又QM=4，且cos∠QHM=

3

9

，
∴tan∠QHM=

QM

MH

=

2 x2+4 2 x+16

x

=

26

，
解得x=

2

，∴MK的长度为

2

．…（15分）
方法2：以B为原点，以BC、BA所在直线为x轴y轴建空间直角坐标系，
则A（0，8，0），M（0，4，0），N（4，0，0），P（0，8，8），Q（0，4，4），
设K（a，b，0），则a+b=4，

AQ

=（0，-4，4），

AK

=(a，-4-a，0)…（9分）
记

n

=(x，y，z)为平面AQK的一个法向量，则

n • AQ =0 n • Azk =0

⇒

y=z ax=(4+a)y

，
取y=z=a则x=4+a，
则

n

=(a+4，a，a)，…（11分）
又平面AKM的一个法向量

m

=(0，0，1)，设二面角Q-AK-M的平面角为θ
则|cosθ|=

| m • n |

| m || n |

=

a

(a+4)2+2a2

=

3

9

，解得a=1，
∴MK的长度为

2

．…（15分）