题目内容
心理学家通过研究学生的学习行为发现;学生的接受能力与老师引入概念和描述问题所用的时间相关,教学开始时,学生的兴趣激增,学生的兴趣保持一段较理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用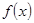 表示学生掌握和接受概念的能力, x表示讲授概念的时间(单位:min),可有以下的关系:
表示学生掌握和接受概念的能力, x表示讲授概念的时间(单位:min),可有以下的关系: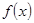
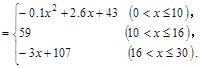
(1)开讲后第5min与开讲后第20min比较,学生的接受能力何时更强一些?
(2)开讲后多少min学生的接受能力最强?能维持多少时间?
(3)若一个新数学概念需要55以上(包括55)的接受能力以及13min时间,那么老师能否在学生一直达到所需接受能力的状态下讲授完这个概念?
(1)开讲后第5min比开讲后第20min,学生接受能力强一些.;(2)6min; (3)详见解析.
解析试题分析:此题考查的是分段函数的基本知识及分段函数图象增减性的应用.第一小题求学生的接受能力最强其实就是要求分段函数的最大值,方法是分别求出各段的最大值取其最大即可.第二小题比较5分钟和15分钟学生的接受能力何时强,方法是把x=5代入第一段函数中,而x=15要代入到第二段函数中,比较大小即可.不同的自变量代入相应的解析式才能符合要求.第三小题考查分段函数图象和增减性,令f(x)=55,第一段函数解得x=6,第二段函数解得x=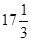 ,关键是从图象上知道6<x<
,关键是从图象上知道6<x<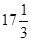
时,f(x)>55,然后求出两个时间之差即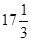 -6=
-6=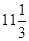 ,其实就是持续的时间,最后和10分钟比较大小即可.
,其实就是持续的时间,最后和10分钟比较大小即可.
试题解析::(1) 2分
2分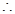 开讲后第5min比开讲后第20min,学生接受能力强一些. 3分
开讲后第5min比开讲后第20min,学生接受能力强一些. 3分
(2)当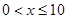 时,
时,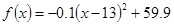 4分
4分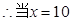 时
时 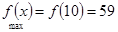 5分
5分
当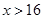 时,
时,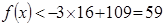 6分
6分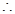 开讲后10mim(包括10mim)学生接受能力最强,能维持6min.7分
开讲后10mim(包括10mim)学生接受能力最强,能维持6min.7分
(3)由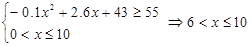 9分
9分
又由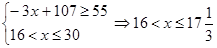 , 11分
, 11分
故接受概念的能力在55以上(包括55)的时间为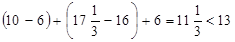
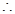 老师不能在学生一直达到所需接受能力的的状态下讲授完这个新概念12分
老师不能在学生一直达到所需接受能力的的状态下讲授完这个新概念12分
考点:根据实际问题选择函数类型.

 名校课堂系列答案
名校课堂系列答案某商场经营一批进价是30元/件的商品,在市场试销中发现,此商品销售价 元与日销售量
元与日销售量 件之间有如下关系:
件之间有如下关系:
| x | 45 | 50 |
| y | 27 | 12 |
 与
与 的一个一次函数关系式
的一个一次函数关系式 ;
;(Ⅱ)若日销售利润为P元,根据(I)中关系写出P关于
 的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?
的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润? 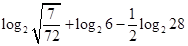 ;
; .
.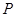 和
和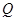 (万元),它们与投入资金
(万元),它们与投入资金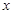 (万元)的关系依次是:其中
(万元)的关系依次是:其中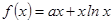 的图象在点
的图象在点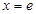 (e为自然对数的底数)处取得极值-1.
(e为自然对数的底数)处取得极值-1.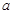 的值;
的值; 对任意
对任意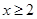 恒成立,求
恒成立,求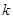 的取值范围.
的取值范围.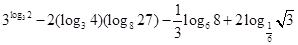 .
.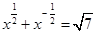 ,求
,求 的值.
的值.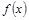 与第x天近似地满足
与第x天近似地满足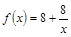 (千人),且参观民俗文化村的游客人均消费
(千人),且参观民俗文化村的游客人均消费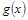 近似地满足
近似地满足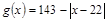 (元).
(元).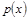 (单位千元,1≤x≤30,
(单位千元,1≤x≤30,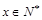 )的函数关系;
)的函数关系;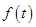 (单位:米)与生长年限t(单位:年)
(单位:米)与生长年限t(单位:年)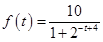 .(设该生物出生时t=0)
.(设该生物出生时t=0)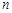 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为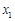 ,
,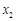 ,
,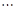 ,
,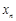 ,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.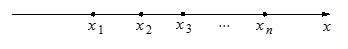
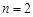 ,每个工作台上只有一名工人,试确定供应站的位置;
,每个工作台上只有一名工人,试确定供应站的位置;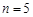 ,工作台从左到右的人数依次为
,工作台从左到右的人数依次为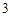 ,
,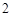 ,
,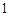 ,
,