题目内容
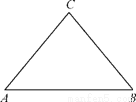
(本小题满分14分)如图，△ABC为一个等腰三角形形状的空地，腰CA的长为3(百米)，底AB的长为4(百米)．现决定在该空地内筑一条笔直的小路EF(宽度不计)，将该空地分成一个四边形和一个三角形，设分成的四边形和三角形的周长相等、面积分别为S1和S2.
(1) 若小路一端E为AC的中点，求此时小路的长度；
(2) 求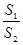
的最小值．
【答案】
解：(1) ∵ E为AC中点，∴ AE＝CE＝
.
∵ ＋3＜＋4，∴ F不在BC上．(2分)
若F在AB上，则AE＋AF＝3－AE＋4－AF＋3，∴ AE＋AF＝5.
∴ AF＝
＜4.(4分)
在△ABC中，cosA＝
.(5分)
在△AEF中，EF2＝AE2＋AF2－2AE·AFcosA＝
＋
－2×××＝
，
∴ EF＝
.(6分) 即小路一端E为AC的中点时小路的长度为 (百米)．(7分)
(2) 若小道的端点E、F点都在两腰上，如图，设CE＝x，CF＝y，
答：最小值是
.(14分)
【解析】略
练习册系列答案
相关题目
(a＞b＞0)，曲线C2的方程为y=
，且曲线C1与C2在第一象限内只有一个公共点P。（1）试用a表示点P的坐标；（2）设A、B是椭圆C1的两个焦点，当a变化时，求△ABP的面积函数S(a)的值域；（3）记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积，试求函数f(a)=min{g(a), S(a)}的表达式。
=2，点（
）在函数
的图像上，其中
=
.
}是等比数列；
，求
及数列{
}的通项公式；
，求数列{
}的前n项和
，并证明
.
天(
)的销售价格(单位：元)为
，第
，已知该商品成本为每件25元.
关于第
的图像在点
处的切线与直线
平行.
，
满足的关系式；
上恒成立，求
（
）