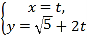Question

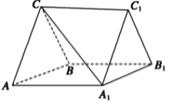
【题目】已知圆，设平面区域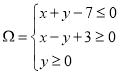，若圆心，且圆与轴相切，则的最小值为__________，的最大值为__________.

Answer 1

【答案】0 37

【解析】

作出不等式组对应的平面区域，利用圆C与x轴相切，得到b=1为定值，此时利用数形结合确定a的取值即可得到结论．

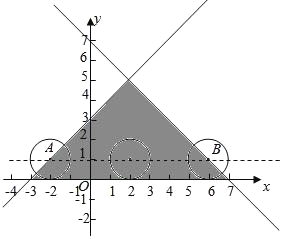
作出不等式组对应的平面区域如图：

圆心为(a,b)，半径为1，

∵圆心C∈Ω，且圆C与x轴相切，

∴b=1,a+2b=a+2,

由y=1及xy+3=0解得A(2,1)，

a+2b的最小值为：0，

则a2+b2=a2+1，

∴要使a2+b2的取得最大值，则只需a最大即可，

由图象可知当圆心C位于B点时，a取值最大，

由y=1及x+y7=0,解得B(6,1)，

∴当a=6,b=1时,a2+b2=36+1=37，即最大值为37，

故答案为：0；37.