题目内容
在数列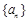 中,前n项和为
中,前n项和为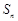 ,且
,且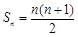 .
.
(Ⅰ)求数列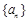 的通项公式;
的通项公式;
(Ⅱ)设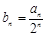 ,数列
,数列 前n项和为
前n项和为 ,求
,求 的取值范围.
的取值范围.
(Ⅰ)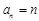 ;(Ⅱ)
;(Ⅱ)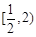 .
.
解析试题分析:(Ⅰ)已知前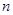 项和公式
项和公式 求
求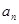 ,则
,则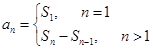 .由此可得数列
.由此可得数列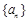 的通项公式.
的通项公式.
(Ⅱ)由等差数列与等比数列的积或商构成的新数列,求和时用错位相消法.在本题中用错位相消法可得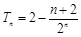 .这也是一个数列,要求数列的范围,首先考查数列的单调性,而考查数列的单调性,一般是考查相邻两项的差的符号.作差易得
.这也是一个数列,要求数列的范围,首先考查数列的单调性,而考查数列的单调性,一般是考查相邻两项的差的符号.作差易得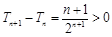 ,所以这是一个递增数列,第一项即为最小值.递增数列有可能无限增大,趋近于无穷大.本题中由于
,所以这是一个递增数列,第一项即为最小值.递增数列有可能无限增大,趋近于无穷大.本题中由于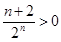 ,所以
,所以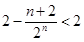 .由此即得
.由此即得 的取值范围.
的取值范围.
试题解析:(Ⅰ)当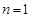 时,
时,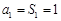 ;
;
当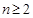 时,
时,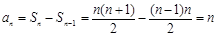 ,经验证,
,经验证, 满足上式.
满足上式.
故数列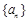 的通项公式
的通项公式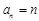 . 4分
. 4分
(Ⅱ)可知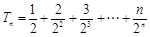 ,
,
则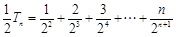 ,
,
两式相减,得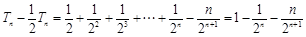 ,
,
所以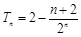 . 8分
. 8分
由于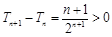 ,则
,则 单调递增,故
单调递增,故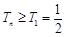 ,
,
又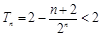 ,
,
故 的取值范围是
的取值范围是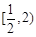 12分
12分
考点:1、等差数列与等比数列;2、错位相消法求和;3、数列的范围.

练习册系列答案
相关题目
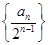 的前n项和.
的前n项和. ABC中,三个内角A,B,C的对边分别为
ABC中,三个内角A,B,C的对边分别为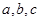 ,且A,B,C成等差数列,
,且A,B,C成等差数列,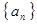 ,满足
,满足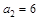 ,
,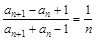
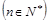 ,
,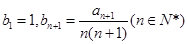 ,求数列
,求数列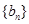 所满足的通项公式;
所满足的通项公式;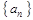 的通项公式;
的通项公式;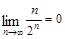 ,设
,设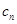 =
=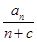
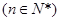 ,常数
,常数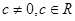 ,若数列
,若数列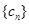 是等差数列,记
是等差数列,记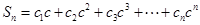 ,求
,求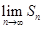 .
.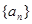 满足
满足 (
( ).
).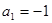 ,
, (
( 和
和 的值,使得数列
的值,使得数列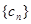 为等比数列;并求此时数列
为等比数列;并求此时数列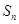 是数列
是数列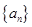 的前
的前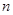 项和,对任意
项和,对任意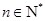 都有
都有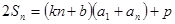 成立, (其中
成立, (其中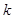 、
、 、
、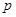 是常数).
是常数).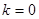 ,
,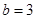 ,
,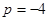 时,求
时,求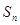 ;
;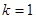 ,
,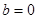 ,
,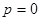 时,
时,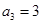 ,
,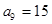 ,求数列
,求数列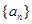 的通项公式;
的通项公式;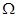 数列”.
数列”.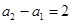 ,试问:是否存在数列
,试问:是否存在数列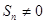 ,且
,且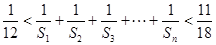 .若存在,求数列
.若存在,求数列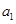 的所
的所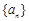 的前n项和为
的前n项和为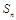 ,且
,且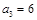 ,
,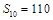 .
. 的通项公式;
的通项公式;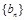 前n项和为
前n项和为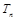 ,且
,且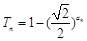 ,令
,令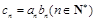 .求数列
.求数列 的前n项和
的前n项和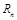 .
.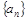 满足:
满足: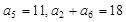 .
.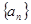 的通项公式;
的通项公式;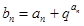 (
(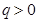 ),求数列
),求数列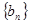 的前n项和
的前n项和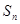 .
.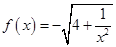 ,数列
,数列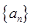 的前
的前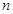 项和为
项和为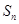 ,点
,点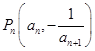 在曲线
在曲线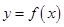 上
上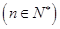 ,且
,且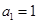 ,
,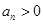 .
.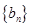 的前
的前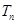 ,且满足
,且满足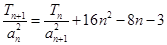 ,
,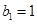 ,求数列
,求数列 ,
,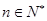 .
.