题目内容
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() .
.
(1)若![]() ,求证:
,求证:![]() ,
,![]() ,
,![]() 必可以被分为1组或2组,使得每组所有数的和小于1;
必可以被分为1组或2组,使得每组所有数的和小于1;
(2)若![]() ,求证:
,求证:![]() ,
,![]() …,
…,![]() ,必可以被分为
,必可以被分为![]() 组
组![]() ,使得每组所有数的和小于1.
,使得每组所有数的和小于1.
【答案】(1)见解析;(2)见解析.
【解析】
(1)先将最大的一个数一组,另两个一组,利用反证法证明这两个较小的数的和小于1;
(2)先将其中介于![]() 和1之间的单独分一组,再把小于
和1之间的单独分一组,再把小于![]() 的数进行拼凑成若干组,保证每组都介于
的数进行拼凑成若干组,保证每组都介于![]() 和1之间,最后剩余的分成一组,再分析介于
和1之间,最后剩余的分成一组,再分析介于![]() 和1之间组数小于等于k即可.
和1之间组数小于等于k即可.
解:(1)不妨设![]()
假设![]() ,则
,则![]()
所以![]()
所以![]() 与
与![]() 矛盾,因此
矛盾,因此![]() ,
,
所以必可分成两组![]() 、
、![]() 使得每组所有数的和小于1
使得每组所有数的和小于1
(2)不妨设![]() ,
,![]()
先将![]() ,
,![]() ,…,
,…,![]() 单独分为一组,再对后面项依次合并分组,使得每组和属于
单独分为一组,再对后面项依次合并分组,使得每组和属于![]() ,最后一组和属于
,最后一组和属于![]() ,不妨设将
,不妨设将![]() ,
,![]() ,…,
,…,![]() 分为
分为![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
,![]() 共
共![]() 组,且其中
组,且其中![]() 组
组![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,最后一组
,最后一组![]()
首先![]() 必小于等于
必小于等于![]() ,否则
,否则![]() ,与
,与![]() ,矛盾
,矛盾
当![]() 时,则
时,则![]()
所以只需将![]() ,
,![]() ,…,
,…,![]() 分为
分为![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
,![]() 即可满足条件;
即可满足条件;
当![]() 时,可将
时,可将![]() 与
与![]() 合成一组,且
合成一组,且![]() ,否则
,否则![]() ,矛盾
,矛盾
此时只需将![]() ,
,![]() ,…,
,…,![]() 分为
分为![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
,![]() 即可满足条件,
即可满足条件,
所以![]() ,
,![]() ,…,
,…,![]() 必可以被分为m组(1≤m≤k),使得每组所有数的和小于1.
必可以被分为m组(1≤m≤k),使得每组所有数的和小于1.

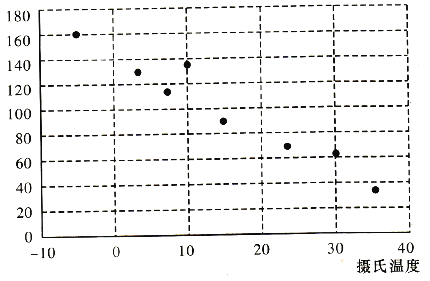
【题目】有一个同学家开了一个小卖部,他为了研究气温对热饮饮料销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的散点图和对比表:
摄氏温度 |
|
|
|
|
|
|
|
|
热饮杯数 |
|
|
|
|
|
|
|
|
(1)从散点图可以发现,各点散布在从左上角到右下角的区域里。因此,气温与当天热饮销售杯数之间成负相关,即气温越高,当天卖出去的热饮杯数越少。统计中常用相关系数![]() 来衡量两个变量之间线性关系的强弱.统计学认为,对于变量
来衡量两个变量之间线性关系的强弱.统计学认为,对于变量![]() 、
、![]() ,如果
,如果![]() ,那么负相关很强;如果
,那么负相关很强;如果![]() ,那么正相关很强;如果
,那么正相关很强;如果![]() ,那么相关性一般;如果
,那么相关性一般;如果![]() ,那么相关性较弱。请根据已知数据,判断气温与当天热饮销售杯数相关性的强弱.
,那么相关性较弱。请根据已知数据,判断气温与当天热饮销售杯数相关性的强弱.
(2)(i)请根据已知数据求出气温与当天热饮销售杯数的线性回归方程;
(ii)记![]() 为不超过
为不超过![]() 的最大整数,如
的最大整数,如![]() ,
,![]() .对于(i)中求出的线性回归方程
.对于(i)中求出的线性回归方程![]() ,将
,将![]() 视为气温与当天热饮销售杯数的函数关系.已知气温
视为气温与当天热饮销售杯数的函数关系.已知气温![]() 与当天热饮每杯的销售利润
与当天热饮每杯的销售利润![]() 的关系是
的关系是![]()
![]() (单位:元),请问当气温
(单位:元),请问当气温![]() 为多少时,当天的热饮销售利润总额最大?
为多少时,当天的热饮销售利润总额最大?
(参考公式)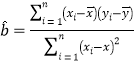 ,
,![]() ,
,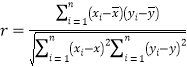
(参考数据)![]() ,
,![]() ,
,![]()
![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
【题目】国家环境标准制定的空气质量指数与空气质量等级对应关系如表:
空气质量指数 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
空气质量等级 | 1级优 | 2级良 | 3级轻 度污染 | 4级中度污染 | 5级重 度污染 | 6级严重污染 |
由全国重点城市环境监测网获得10月份某五天甲城市和乙城市的空气质量指数数据用茎叶图表示如图:
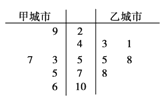
(1)试根据上面的统计数据,计算甲、乙两个城市的空气质量指数的方差;
(2)试根据上面的统计数据,估计甲城市某一天空气质量等级为2级良的概率;
(3)分别从甲城市和乙城市的统计数据中任取一个,试求两个城市空气质量等级相同的概率.供参考数据:292+532+572+752+1062=23760,432+412+552+582+782=16003