题目内容
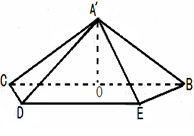
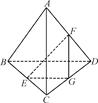
如图,棱柱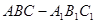 中,四边形
中,四边形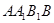 是菱形,四边形
是菱形,四边形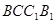 是矩形,
是矩形,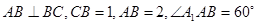 .
.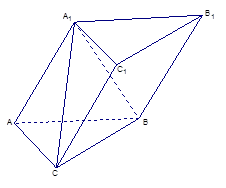
(1)求证:平面 ;
;
(2)求点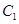 到平面
到平面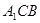 的距离;
的距离;
(3)求直线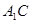 与平面
与平面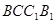 所成角的正切值.
所成角的正切值.
(1)证明过程详见试题解析;(2)点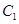 到平面
到平面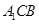 的距离为
的距离为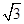 ;(3)直线
;(3)直线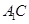 与平面
与平面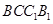 所成角的正切值为
所成角的正切值为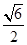 .
.
解析试题分析:(1)先证明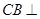 面
面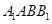 ,又
,又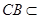 面
面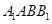 ,∴平面
,∴平面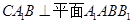 ;(2)先求出
;(2)先求出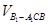 ,即可知点
,即可知点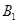 到面
到面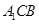 的距离,而点
的距离,而点 到面
到面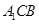 的距离相等,所以点
的距离相等,所以点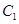 到平面
到平面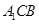 的距离为
的距离为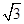 ;(3)先找出
;(3)先找出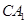 在面
在面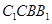 的射影
的射影 ,
,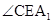 为直线
为直线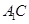 与平面
与平面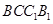 所成线面角,放在
所成线面角,放在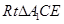 中即可求出直线
中即可求出直线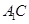 与平面
与平面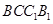 所成角的正切值为
所成角的正切值为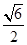 .
.
试题解析:(1)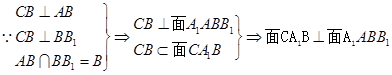 4分
4分
(2)解: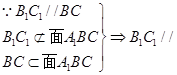 面
面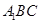 ,所以点
,所以点 到面
到面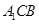 的距离相等, 6分
的距离相等, 6分
设点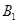 到面
到面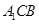 的距离相等,则
的距离相等,则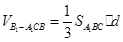
∵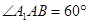 ,∴
,∴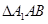 为正三角形,
为正三角形,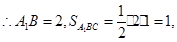
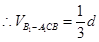 7分
7分
又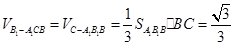 8分
8分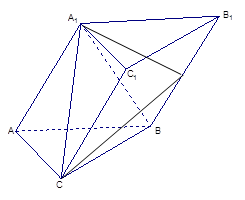
∴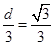 ,∴
,∴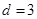 ,点
,点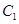 到平面
到平面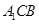 的距离为
的距离为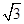 . 9分
. 9分
(3)解:过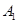 作
作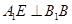 ,垂足为
,垂足为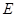 10分
10分 面
面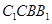 12分
12分
∴ 为
为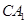 在面
在面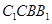 的射影,
的射影,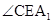 为直线
为直线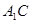 与平面
与平面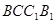 所成线面角, 13分
所成线面角, 13分
在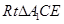 中,
中,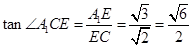 ,
,
所以直线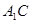 与平面
与平面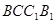 所成角的正切值为
所成角的正切值为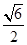 . 14分
. 14分
考点:面面垂直的判定定理、直线与平面所成的角、空间想象能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
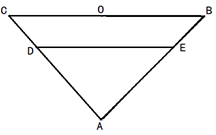
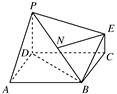
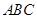 中,
中, 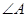 =900 ,
=900 ,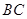 ="6,"
="6," 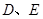 分别是
分别是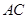 ,
,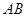 上的点,
上的点,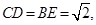
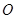 为
为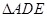 沿
沿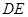 折起,得到如图所示的四棱椎
折起,得到如图所示的四棱椎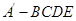 ,其中
,其中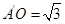
 ;
;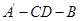 的平面角的余弦值.
的平面角的余弦值.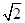 EF.求证:
EF.求证:
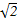 .等边三角形ADB以AB为轴转动.
.等边三角形ADB以AB为轴转动.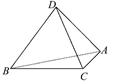
 中,
中, ,点
,点 是
是 的中点。
的中点。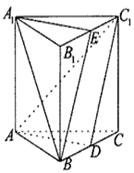
 ∥平面
∥平面
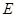 是
是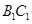 的中点,求证:平面
的中点,求证:平面 平面
平面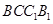 .
.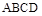 与
与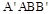 都是边长为
都是边长为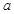 的正方形,点E是
的正方形,点E是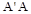 的中点,
的中点,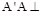 平面
平面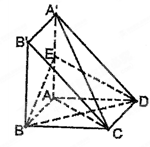
 平面
平面 ;
;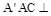 平面
平面