题目内容
【题目】已知动圆![]() 经过点
经过点![]() ,且动圆
,且动圆![]() 被
被![]() 轴截得的弦长为4,记圆心
轴截得的弦长为4,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的标准方程;
的标准方程;
(2)过![]() 轴下方一点
轴下方一点![]() 向曲线
向曲线![]() 作切线,切点记作
作切线,切点记作![]() 、
、![]() ,直线
,直线![]() 交曲线
交曲线![]() 于点
于点![]() ,若直线
,若直线![]() 、
、![]() 的斜率乘积为
的斜率乘积为![]() ,点
,点![]() 在以
在以![]() 为直径的圆上,求点
为直径的圆上,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设![]() ,动圆
,动圆![]() 被
被![]() 轴截得的弦长为4,则
轴截得的弦长为4,则![]() ,从而得到答案.
,从而得到答案.
(2)设直线![]() :
:![]() ,
,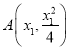 ,
, ,求出过
,求出过![]() 的切线方程,方程联立,结合直线
的切线方程,方程联立,结合直线![]() 、
、![]() 的斜率乘积为
的斜率乘积为![]() ,用
,用![]() 表示出点
表示出点![]() 的坐标,点
的坐标,点![]() 在以
在以![]() 为直径的圆上,则
为直径的圆上,则![]() ,建立关于
,建立关于![]() 的方程求解即可.
的方程求解即可.
解:(1)设![]() ,则
,则![]() ,
,
![]() ,即
,即![]() ,
,
所以曲线的标准方程为:![]() .
.
(2)设直线![]() :
:![]() ,
,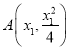 ,
, ,
,
![]() ,
,
过点![]() 的切线方程为:
的切线方程为:![]() ,
,
过点![]() 的切线方程为:
的切线方程为:![]() ,
,
联立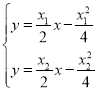 ,解得
,解得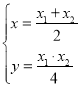 ,
,
所以,点![]() ,
,
 ,
,
所以点![]() ,则又
,则又![]() ,则
,则![]() ,
,
由![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
代入抛物线![]() ,可得
,可得![]() ,
,
点![]() 在以
在以![]() 为直径的圆上,则
为直径的圆上,则![]() ,
,
![]()
![]() ,
,
![]() ,
,
整理得![]() ,
,
所以,点![]() 的坐标为:
的坐标为:![]() .
.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
【题目】噪声污染已经成为影响人们身体健康和生活质量的严重问题,为了了解声音强度![]() (单位:分贝)与声音能量(单位:
(单位:分贝)与声音能量(单位:![]() )之间的关系,将测量得到的声音强度
)之间的关系,将测量得到的声音强度![]() 和声音能量
和声音能量![]() (
(![]() =1,2…,10)数据作了初步处理,得到如图散点图及一些统计量的值.
=1,2…,10)数据作了初步处理,得到如图散点图及一些统计量的值.

|
|
|
|
|
| 45.7 |
|
| 0.51 |
|
| |||
| 5.1 | |||
表中![]() ,
,![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为声音强度
哪一个适宜作为声音强度![]() 关于声音能量的回归方程类型?(给出判断即可,不必说明理由)
关于声音能量的回归方程类型?(给出判断即可,不必说明理由)
(2)根据表中数据,求声音强度![]() 关于声音能量的回归方程;
关于声音能量的回归方程;
(3)当声音强度大于60分贝时属于噪音,会产生噪音污染,城市中某点![]() 共受到两个声源的影响,这两个声源的声音能量分别是
共受到两个声源的影响,这两个声源的声音能量分别是![]() 和
和![]() ,且
,且![]() .己知点
.己知点![]() 的声音能量等于声音能量
的声音能量等于声音能量![]() 与
与![]() 之和.请根据(1)中的回归方程,判断
之和.请根据(1)中的回归方程,判断![]() 点是否受到噪音污染的干扰,并说明理由.
点是否受到噪音污染的干扰,并说明理由.
附:对于一组数据![]() .其回归直线
.其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: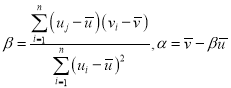 .
.