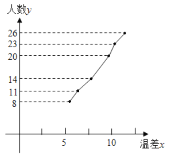
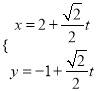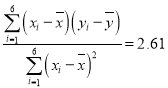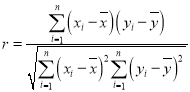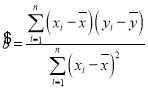题目内容
【题目】若存在![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立,则函数
恒成立,则函数![]() 在
在![]() 上有下界,其中
上有下界,其中![]() 为函数
为函数![]() 的一个下界;若存在
的一个下界;若存在![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立,则函数
恒成立,则函数![]() 在
在![]() 上有上界,其中
上有上界,其中![]() 为函数
为函数![]() 的一个上界.如果一个函数既有上界又有下界,那么称该函数有界.
的一个上界.如果一个函数既有上界又有下界,那么称该函数有界.
下述四个结论:①1不是函数![]() 的一个下界;②函数
的一个下界;②函数![]() 有下界,无上界;③函数
有下界,无上界;③函数![]() 有上界,无下界;④函数
有上界,无下界;④函数![]() 有界.
有界.
其中所有正确结论的编号是( )
A.①②B.②④C.③④D.②
【答案】B
【解析】
根据函数上界、下界及有界的概念,利用导数判断函数的单调性并求最值,结合选项,利用排除法,对结论①②③④进行逐项判断即可.
对于结论①:当![]() 时,由对勾函数的性质知,函数
时,由对勾函数的性质知,函数![]() 恒成立,所以可得函数
恒成立,所以可得函数![]() 对任意
对任意![]() 恒成立,即1是函数
恒成立,即1是函数![]() 的一个下界,故结论①错误;
的一个下界,故结论①错误;
对于结论②:因为函数![]() ,
,![]() ,所以
,所以![]() ,所以当
,所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,故函数
,故函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,所以当
上单调递增,所以当![]() 时,函数
时,函数![]() 有最小值为
有最小值为![]() ,即存在
,即存在![]() 使任意
使任意![]() ,
,![]()
![]() 恒成立,故函数
恒成立,故函数![]() 有下界;当
有下界;当![]() 时,函数
时,函数![]() ,故函数
,故函数![]() 无上界;因此结论②正确;
无上界;因此结论②正确;
对于结论③:因为函数![]() ,所以
,所以![]() ,所以当
,所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;所以函数
;所以函数![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减,当
上单调递减,当![]() 时,
时,![]() ,所以函数
,所以函数![]() 无上界,故结论③错误;
无上界,故结论③错误;
对于结论④:因为函数![]() 为周期函数,且
为周期函数,且![]() ,当
,当![]() 时,
时,![]() ,该函数为振荡函数,所以对任意
,该函数为振荡函数,所以对任意![]() 函数
函数![]() 恒成立,故函数
恒成立,故函数![]() 有界,故结论④正确.
有界,故结论④正确.
故选:B

 阅读快车系列答案
阅读快车系列答案【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
表1:甲套设备的样本的频数分布表
质量指标值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
频数 | 1 | 5 | 18 | 19 | 6 | 1 |
图1:乙套设备的样本的频率分布直方图
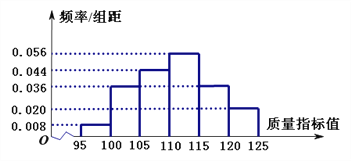
(Ⅰ)将频率视为概率. 若乙套设备生产了5000件产品,则其中的不合格品约有多少件;
(Ⅱ)填写下面列联表,并根据列联表判断是否有90%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关;
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
(Ⅲ)根据表1和图1,对两套设备的优劣进行比较.
附:

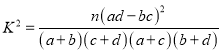 .
.