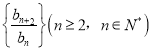Question

【题目】在平面直角坐标系中,长度为2的线段EF的两端点E、F分别在两坐标轴上运动.

(1)求线段EF的中点G的轨迹C的方程；

(2)设轨迹C与轴交于两点,P是轨迹C上异于的任意一点,直线交直线于M点,直线交直线于N点,求证:以MN为直径的圆C总过定点,并求出定点坐标.

Answer 1

【答案】（1）;（2）或.

【解析】

（1）设,把两点坐标用表示,结合两点间的距离公式,即可求得G的轨迹C的方程;

（2）由（1）求出两点坐标,设,分别求出直线、直线的方程,进而表示出M、N两点坐标,求出以MN为直径的圆C的方程,根据对称性,定点在轴上,求出圆C与轴的交点,即为所求.

（1）设,由中点坐标公式得,

,整理得,,

线段EF的中点G的轨迹C的方程为;

（2）由（1）得,,设,

,直线方程为:，

令,得,,同理可求，

中点坐标为,

以MN为直径的圆C的方程为

令，得

,圆C总过定点,定点坐标为或.