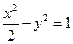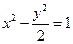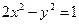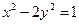题目内容
(本小题满分12分)已知双曲线C: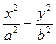 =1(a>0,b>0)的一条准线方程为x=
=1(a>0,b>0)的一条准线方程为x=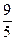 ,一个顶点到一条渐近线的距离为
,一个顶点到一条渐近线的距离为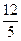 .
.
(1)求双曲线C的方程;
(2)动点P到双曲线C的左顶点A和右焦点F的距离之和为常数(大于|AF|),且cosAPF的最小值为-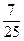 ,求动点P的轨迹方程.
,求动点P的轨迹方程.
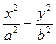 =1(a>0,b>0)的一条准线方程为x=
=1(a>0,b>0)的一条准线方程为x=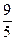 ,一个顶点到一条渐近线的距离为
,一个顶点到一条渐近线的距离为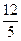 .
.(1)求双曲线C的方程;
(2)动点P到双曲线C的左顶点A和右焦点F的距离之和为常数(大于|AF|),且cosAPF的最小值为-
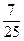 ,求动点P的轨迹方程.
,求动点P的轨迹方程.(1)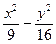 =1;(2)
=1;(2)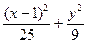 ="1. "
="1. "
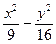 =1;(2)
=1;(2)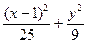 ="1. "
="1. " 解:(1)易求得方程为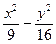 ="1. " 5分
="1. " 5分
(2)A、F是定点,由圆锥曲线的定义知,点P的轨迹为椭圆.设其长轴为2a,短轴为2b,焦距为2c=8,在△PAF中,应用余弦定理研究∠APF的余弦,应用基本不等式可知,cosAPF≥1-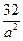 ,
,
当且仅当|PA|=|PF|=a时取等号,故a2=25,b2=9,求出椭圆中心的坐标为(1,0),则所求方程为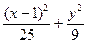 ="1. " ……………… 12分
="1. " ……………… 12分
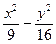 ="1. " 5分
="1. " 5分(2)A、F是定点,由圆锥曲线的定义知,点P的轨迹为椭圆.设其长轴为2a,短轴为2b,焦距为2c=8,在△PAF中,应用余弦定理研究∠APF的余弦,应用基本不等式可知,cosAPF≥1-
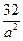 ,
,当且仅当|PA|=|PF|=a时取等号,故a2=25,b2=9,求出椭圆中心的坐标为(1,0),则所求方程为
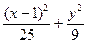 ="1. " ……………… 12分
="1. " ……………… 12分
练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
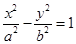 (
(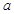 >0,
>0, 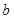 >0)的离心率为2,一个焦点与抛物线
>0)的离心率为2,一个焦点与抛物线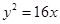 的焦点相同,则双曲线的方程为( )
的焦点相同,则双曲线的方程为( )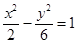
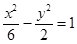
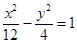
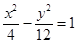
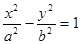 焦点
焦点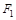 ,
,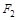 , 过点
, 过点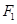 作垂直于
作垂直于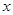 轴的直线交双曲线于
轴的直线交双曲线于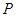 点,且
点,且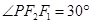 ,则双曲线的渐近线是()
,则双曲线的渐近线是()
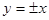
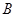
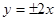

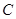
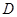
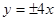
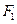 ,
,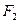 为双曲线左,右焦点,以双曲线右支上任意一点P为圆心,以
为双曲线左,右焦点,以双曲线右支上任意一点P为圆心,以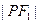 为半径的圆与以
为半径的圆与以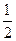
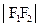 为半径的圆内切,则双曲线两条渐近线的夹角是
为半径的圆内切,则双曲线两条渐近线的夹角是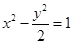 的焦点为
的焦点为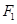 、
、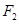 ,点M在双曲线上且
,点M在双曲线上且 ,则点
,则点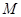 到
到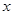 轴的距离为( )
轴的距离为( )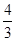
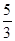
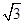
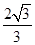
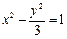 的左、右焦点,△ABC 的顶点
的左、右焦点,△ABC 的顶点 ,则
,则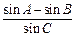 的值是 ▲
的值是 ▲ 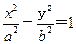 的两焦点为F1、F2,点P在双曲线上,∠F1PF2的平分线分线段F1F2的比为5 :1,则双曲线离心率的取值范围是
的两焦点为F1、F2,点P在双曲线上,∠F1PF2的平分线分线段F1F2的比为5 :1,则双曲线离心率的取值范围是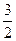 ]
]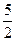 ]
]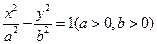 的离心率为
的离心率为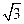 ,且它的两焦点到直线
,且它的两焦点到直线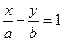 的距离之和为2,则该比曲线方程是
的距离之和为2,则该比曲线方程是