题目内容
函数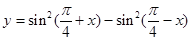 的值域是
的值域是
A.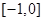 | B.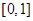 | C.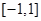 | D.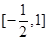 |
C
解析试题分析:根据题意,由于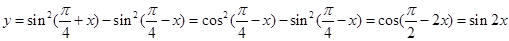 ,可知函数的值域,结合正弦函数的性质可知,最小值为-1,最大值为1,故答案为
,可知函数的值域,结合正弦函数的性质可知,最小值为-1,最大值为1,故答案为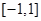 ,选C.
,选C.
考点:三角函数的性质
点评:主要是考查了三角函数的值域的求解,属于基础题。

练习册系列答案
相关题目
函数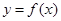 的图像如图所示,
的图像如图所示,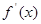 为
为 的导函数,则
的导函数,则 ,
,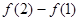 的大小关系是()
的大小关系是()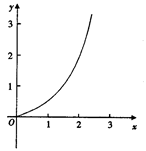
A.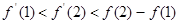 |
B.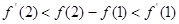 |
C.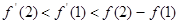 |
D.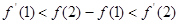 |
设f(x)为周期是2的奇函数,当 时,f(x)=x(x+1),则当
时,f(x)=x(x+1),则当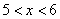 时,f(x)的表达式为
时,f(x)的表达式为
| A.(x-5)(x-4) | B.(x-6)(x-5) | C.(x-6)(5-x) | D.(x-6)(7-x) |
设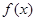 为定义在
为定义在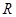 上的奇函数,当
上的奇函数,当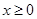 时,
时,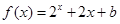 (
( 为常数),则
为常数),则
| A.-3 | B.-1 | C.1 | D.3 |
若 ,则( )
,则( )
A.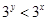 | B.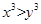 | C. | D.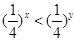 |
函数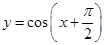 ,
,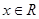 ( )
( )
| A.是偶函数 | B.是奇函数 |
| C.既不是奇函数也不是偶函数 | D.既是奇函数也是偶函数 |
已知R上可导函数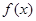 的图象如图所示,则不等式
的图象如图所示,则不等式 的解集为
的解集为
A.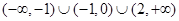 | B. |
C.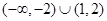 | D.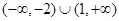 |
函数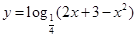 的单调递增区间是( )
的单调递增区间是( )
A.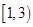 | B.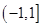 | C.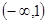 | D. |
若函数 的零点与
的零点与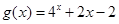 的零点之差的绝对值不超过
的零点之差的绝对值不超过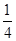 ,则
,则 可以是
可以是
A. =4x-1 =4x-1 | B. =(x-1)2 =(x-1)2 |
C. =ex-2 =ex-2 | D.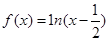 |