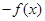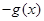题目内容
设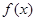 为定义在
为定义在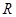 上的奇函数,当
上的奇函数,当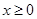 时,
时,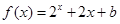 (
( 为常数),则
为常数),则
| A.-3 | B.-1 | C.1 | D.3 |
A
解析试题分析:∵当x≥0时,f(x)=2x+2x+a,∴f(1)=4+a
∵f(x)是定义在R上的奇函数,∴f(0)=1+0+a=0,∴a=-1,
∴f(-1)=-f(1)=-4-a=-3,故选A。
考点:本题主要考查函数的奇偶性。
点评:简单题,奇函数在x=0处有定义,则有f(0)=0。

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 是以
是以 为周期的奇函数,若
为周期的奇函数,若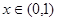 时,
时, ,则
,则 在区间
在区间 上是( )
上是( )
A.增函数且 | B.减函数且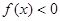 |
C.增函数且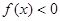 | D.减函数且 |
如图所示,曲线是函数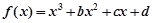 的大致图象,则
的大致图象,则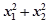 等于( )
等于( )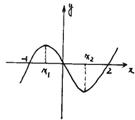
A.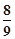 | B.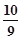 | C.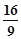 | D.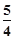 |
已知函数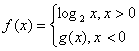 是偶函数,则
是偶函数,则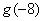 的值等于( )
的值等于( )
| A.-8 | B.-3 | C.3 | D.8 |
函数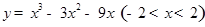 有 ( )
有 ( )
A.最大值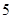 ,最小值-22 ,最小值-22 | B.最大值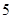 ,最小值-2 ,最小值-2 |
C.最大值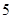 ,无最小值 ,无最小值 | D.最小值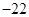 ,无最大值 ,无最大值 |
函数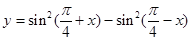 的值域是
的值域是
A.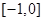 | B.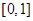 | C.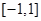 | D.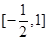 |
已知函数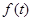 是奇函数且是
是奇函数且是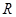 上的增函数,若
上的增函数,若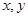 满足不等式
满足不等式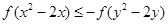 ,则
,则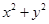 的最大值是( )
的最大值是( )
A. | B.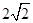 | C.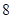 | D.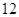 |
函数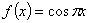 与函数
与函数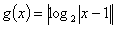 的图象所有交点的横坐标之和为
的图象所有交点的横坐标之和为
A.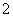 | B.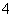 |
C.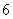 | D.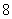 |
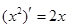 ,
,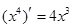 ,
,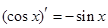 ,由归纳推理可得:若定义在R上的函数
,由归纳推理可得:若定义在R上的函数 满足
满足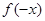 =
=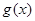 为
为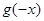 =( )
=( )