题目内容
函数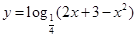 的单调递增区间是( )
的单调递增区间是( )
A.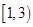 | B.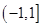 | C.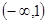 | D. |
A
解析试题分析:根据题意,由于函数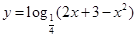 中,
中,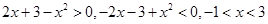 ,那么外层是递减函数,要求递增区间,只要求解内层的增区间即可,内层二次函数,开口向下,对称轴x=1,那么可知,
,那么外层是递减函数,要求递增区间,只要求解内层的增区间即可,内层二次函数,开口向下,对称轴x=1,那么可知,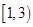 上递减,故可知函数的增区间为A
上递减,故可知函数的增区间为A
考点:函数的单调性
点评:解决的关键是根据对数真数大于零,得到定义域和复合函数单调性来判定,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数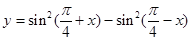 的值域是
的值域是
A.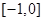 | B.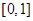 | C.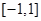 | D.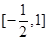 |
若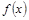 是偶函数,且当
是偶函数,且当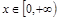 时,
时,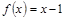 ,则
,则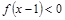 的解集是( )
的解集是( )
A.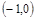 | B.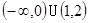 | C. | D.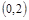 |
若函数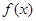 为奇函数,且当
为奇函数,且当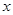 >0时
>0时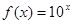 ,则
,则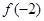 的值是( )
的值是( )
A.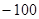 | B.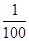  | C.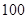 | D.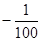 |
当0< ≤
≤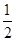 时,
时,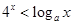 ,则a的取值范围是
,则a的取值范围是
A.(0, ) ) | B.( ,1) ,1) | C.(1,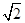 ) ) | D.(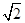 ,2) ,2) |
已知函数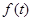 是奇函数且是
是奇函数且是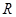 上的增函数,若
上的增函数,若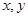 满足不等式
满足不等式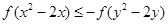 ,则
,则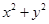 的最大值是( )
的最大值是( )
A. | B.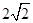 | C.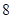 | D. |
如图为函数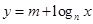 的图象,其中
的图象,其中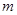 、
、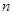 为常数,则下列结论正确( )
为常数,则下列结论正确( )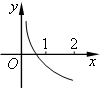
A. , ,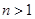 | B. , ,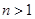 |
C. , , | D. , , |
函数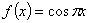 与函数
与函数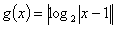 的图象所有交点的横坐标之和为
的图象所有交点的横坐标之和为
A.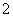 | B.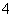 |
C.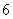 | D.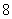 |
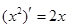 ,
,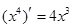 ,
,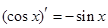 ,由归纳推理可得:若定义在R上的函数
,由归纳推理可得:若定义在R上的函数 满足
满足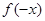 =
=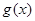 为
为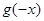 =( )
=( )