题目内容
定义在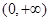 上的函数
上的函数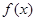 ,对于任意的m,n∈(0,+∞),都有
,对于任意的m,n∈(0,+∞),都有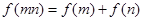 成立,当x>1时,
成立,当x>1时,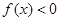 .
.
(1)求证:1是函数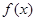 的零点;
的零点;
(2)求证: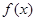 是(0,+∞)上的减函数;
是(0,+∞)上的减函数;
(3)当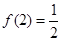 时,解不等式
时,解不等式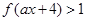 .
.
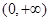 上的函数
上的函数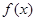 ,对于任意的m,n∈(0,+∞),都有
,对于任意的m,n∈(0,+∞),都有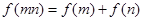 成立,当x>1时,
成立,当x>1时,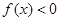 .
.(1)求证:1是函数
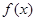 的零点;
的零点;(2)求证:
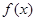 是(0,+∞)上的减函数;
是(0,+∞)上的减函数;(3)当
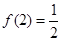 时,解不等式
时,解不等式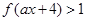 .
.(3)当a=0时,解集为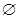 ;当a>0时,解集为
;当a>0时,解集为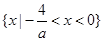 ;
;
当a<0时,解集为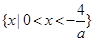 ..
..
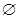 ;当a>0时,解集为
;当a>0时,解集为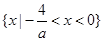 ;
;当a<0时,解集为
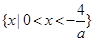 ..
..(1)赋值法,求得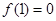 ;(2)注意构造
;(2)注意构造 ;
;
(3)由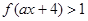 等价于
等价于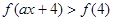 ,分类讨论.
,分类讨论.
解:(1)对于任意的正实数m,n都有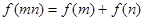 成立,
成立,
所以令m=n=1,则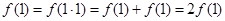 .
.
∴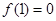 ,即1是函数f(x)的零点. (3分)
,即1是函数f(x)的零点. (3分)
(2)设0<x1<x2,则由于对任意正数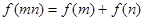 ,
,
所以 ,即
,即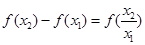
又当x>1时,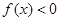 ,而
,而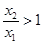 .所以
.所以 .
.
从而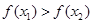 ,因此
,因此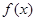 在(0,+∞)上是减函数. (7分)
在(0,+∞)上是减函数. (7分)
(3)根据条件有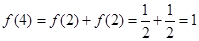 ,
,
所以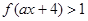 等价于
等价于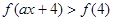 .
.
再由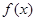 是定义在(0,+∞)上的减函数,所以0<ax+4<4.即
是定义在(0,+∞)上的减函数,所以0<ax+4<4.即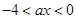 . (9分)
. (9分)
当a=0时,-4<0<0不成立,此时不等式的解集为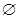 ; (10分)
; (10分)
当a>0时,-4<ax<0,即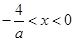 ,此时不等式的解集为
,此时不等式的解集为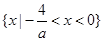 ;
;
当a<0时,-4<ax<0,即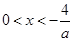 ,此时不等式的解集为
,此时不等式的解集为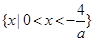 .(12分)
.(12分)
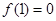 ;(2)注意构造
;(2)注意构造 ;
;(3)由
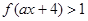 等价于
等价于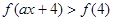 ,分类讨论.
,分类讨论.解:(1)对于任意的正实数m,n都有
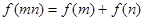 成立,
成立,所以令m=n=1,则
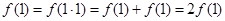 .
.∴
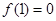 ,即1是函数f(x)的零点. (3分)
,即1是函数f(x)的零点. (3分)(2)设0<x1<x2,则由于对任意正数
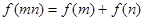 ,
,所以
 ,即
,即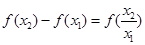
又当x>1时,
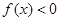 ,而
,而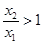 .所以
.所以 .
.从而
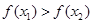 ,因此
,因此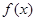 在(0,+∞)上是减函数. (7分)
在(0,+∞)上是减函数. (7分)(3)根据条件有
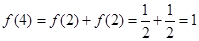 ,
,所以
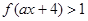 等价于
等价于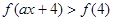 .
.再由
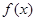 是定义在(0,+∞)上的减函数,所以0<ax+4<4.即
是定义在(0,+∞)上的减函数,所以0<ax+4<4.即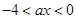 . (9分)
. (9分)当a=0时,-4<0<0不成立,此时不等式的解集为
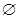 ; (10分)
; (10分)当a>0时,-4<ax<0,即
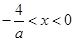 ,此时不等式的解集为
,此时不等式的解集为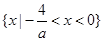 ;
;当a<0时,-4<ax<0,即
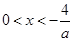 ,此时不等式的解集为
,此时不等式的解集为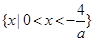 .(12分)
.(12分)
练习册系列答案
相关题目
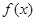 在
在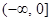 上是减函数,则不等式
上是减函数,则不等式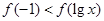 的解集是
的解集是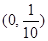
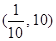
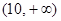
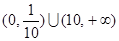
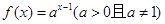
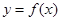 的图象经过P(3,4)点,求a的值;
的图象经过P(3,4)点,求a的值;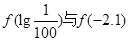 大小,并写出比较过程;
大小,并写出比较过程;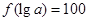 ,求a的值.
,求a的值.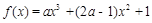 ,当
,当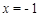 时,函数
时,函数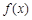 取得极值.
取得极值.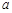 的值;
的值;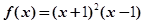 ,
,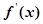 ;
; 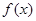 的单调区间;
的单调区间; 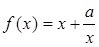 且
且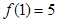 .
. 的值;
的值; 在
在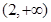 上的单调性,并证明你的结论.
上的单调性,并证明你的结论.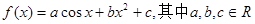 ,适当地选取
,适当地选取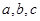 的一组值计算
的一组值计算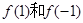 ,所得出的正确结果只可能是( )
,所得出的正确结果只可能是( ) 恒成立,则m的取值范围是 .
恒成立,则m的取值范围是 .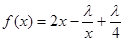 在(1,+∞)上是增函数,则实数
在(1,+∞)上是增函数,则实数  的取值范围是( )
的取值范围是( )