Question

【题目】已知曲线T上的任意一点到两定点的距离之和为，直线l交曲线T于A、B两点，为坐标原点.

（1）求曲线的方程；

（2）若不过点且不平行于坐标轴，记线段AB的中点为M，求证：直线的斜率与l的斜率的乘积为定值；

（3）若OAOB，求△面积的取值范围.

Answer 1

【答案】（1）（2）证明过程详见解析（3）

【解析】

（1）利用椭圆的定义可知曲线为的椭圆，直接写出椭圆的方程．

（2）设直线l：y=kx+b，（k≠0，b≠0），A（x1，y1），B（x2，y2），，联立直线方程与椭圆方程，通过韦达定理求解KOM，然后推出直线OM的斜率与l的斜率的乘积为定值．

（3）当直线OA，OB分别与坐标轴重合时，△AOB的面积，当直线OA，OB的斜率均存在且不为零时，设OA：y＝kx，OB：y，将y＝kx代入椭圆C，得到A点坐标，同理得到B点坐标，由利用换元法结合已知条件能求出△AOB的面积的取值范围．

解：（1）由题意知曲线是以原点为中心，长轴在轴上的椭圆，

设其标准方程为，则有，

所以，∴ .

（2）证明：设直线的方程为，

设

则由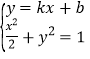 可得，即

∴，∴ ，

，

，

∴直线的斜率与 的斜率的乘积=为定值

（3）当直线、分别与坐标轴重合时，易知的面积，

当直线、的斜率均存在且不为零时，设直线、的方程为：， 点，

由 可得，

∴，代入得 ，

同理可得，

∴

令，，

则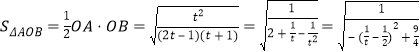

由知 ，

综上可知， .