题目内容
(本小题满分9分)平行四边形ABCD中,AB=2,AD=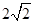 ,且
,且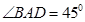 ,以BD为折线,把
,以BD为折线,把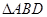 折起,使平面
折起,使平面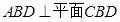 ,连AC.
,连AC.
(Ⅰ)求证: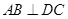 (Ⅱ)求二面角B-AC-D平面角的大小;
(Ⅱ)求二面角B-AC-D平面角的大小;
(Ⅲ)求四面体ABCD外接球的体积.
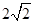 ,且
,且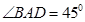 ,以BD为折线,把
,以BD为折线,把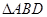 折起,使平面
折起,使平面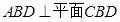 ,连AC.
,连AC.(Ⅰ)求证:
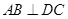 (Ⅱ)求二面角B-AC-D平面角的大小;
(Ⅱ)求二面角B-AC-D平面角的大小;(Ⅲ)求四面体ABCD外接球的体积.

(1)见解析;(2)二面角B-AC-D的大小是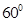 ;(3)
;(3)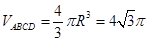 .
.
 ;(3)
;(3)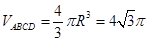 .
. (I)通过证明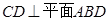 即可.
即可.
(II)由于本题容易建系所以可以通过向量法求解二面角,先求出二面角二个面的法向量,然后根据法向量的夹角与二面角相等或互补求二面角.
(III)解本小题的关键是确定球心位置在AD的中点.
解:在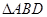 中,
中,
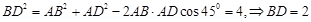 , 易得
, 易得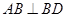 ,
,
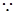 面
面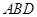
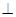 面
面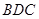
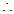
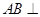 面
面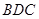
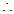
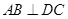 …3分
…3分
在四面体ABCD中,以D为原点,DB为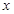 轴,DC为
轴,DC为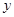 轴,过D垂直于平面BDC的射线为
轴,过D垂直于平面BDC的射线为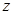 轴,建立如图空间直角坐标系.
轴,建立如图空间直角坐标系.
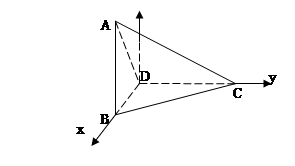 则D(0,0,0),B(2,0,0),C(0,2,0),A(2,0,2)
则D(0,0,0),B(2,0,0),C(0,2,0),A(2,0,2)
(2)设平面ABC的法向量为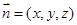 ,而
,而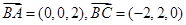 ,
,
由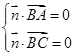 得:
得: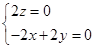 ,取
,取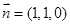 .
.
再设平面DAC的法向量为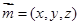 ,而
,而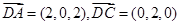 ,
,
由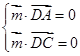 得:
得: ,取
,取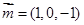 ,
,
所以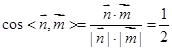 ,所以二面角B-AC-D的大小是
,所以二面角B-AC-D的大小是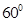 …7分
…7分
(3)由于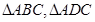 均为直角三角形,故四面体ABCD的外接球球心在AD中点,
均为直角三角形,故四面体ABCD的外接球球心在AD中点,
又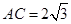 ,所以球半径
,所以球半径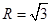 ,得
,得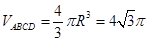 . …9分
. …9分
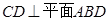 即可.
即可.(II)由于本题容易建系所以可以通过向量法求解二面角,先求出二面角二个面的法向量,然后根据法向量的夹角与二面角相等或互补求二面角.
(III)解本小题的关键是确定球心位置在AD的中点.
解:在
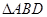 中,
中,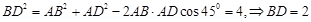 , 易得
, 易得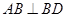 ,
,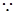 面
面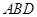
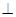 面
面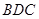
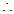
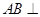 面
面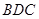
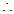
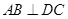 …3分
…3分在四面体ABCD中,以D为原点,DB为
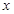 轴,DC为
轴,DC为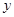 轴,过D垂直于平面BDC的射线为
轴,过D垂直于平面BDC的射线为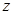 轴,建立如图空间直角坐标系.
轴,建立如图空间直角坐标系.
|
 则D(0,0,0),B(2,0,0),C(0,2,0),A(2,0,2)
则D(0,0,0),B(2,0,0),C(0,2,0),A(2,0,2)(2)设平面ABC的法向量为
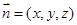 ,而
,而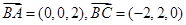 ,
,由
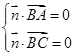 得:
得: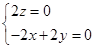 ,取
,取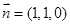 .
.再设平面DAC的法向量为
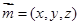 ,而
,而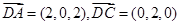 ,
,由
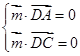 得:
得: ,取
,取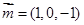 ,
,所以
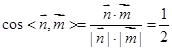 ,所以二面角B-AC-D的大小是
,所以二面角B-AC-D的大小是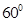 …7分
…7分(3)由于
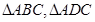 均为直角三角形,故四面体ABCD的外接球球心在AD中点,
均为直角三角形,故四面体ABCD的外接球球心在AD中点,又
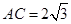 ,所以球半径
,所以球半径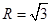 ,得
,得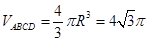 . …9分
. …9分
练习册系列答案
相关题目
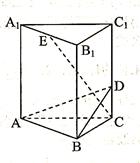
 是等腰直角三角形,
是等腰直角三角形,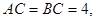
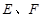 分别为
分别为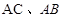 的中点,将△
的中点,将△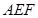 沿
沿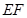 折起,使
折起,使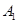 在平面
在平面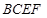 上的射影
上的射影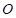 恰好为
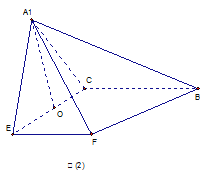
恰好为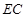 的中点,得到图(2)。
的中点,得到图(2)。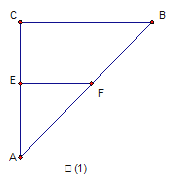
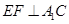 ;(Ⅱ)求三棱锥
;(Ⅱ)求三棱锥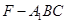 的体积。
的体积。




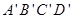 如图所示,其中
如图所示,其中 ,
,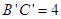 ,
,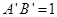 ,求直角梯形以BC为旋转轴旋转一周形成的几何体的表面积。
,求直角梯形以BC为旋转轴旋转一周形成的几何体的表面积。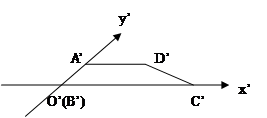
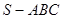 的所有棱长均为2,D是SA 的中点,E是BC 的中点,则
的所有棱长均为2,D是SA 的中点,E是BC 的中点,则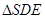 绕直线SE 转一周所得到的旋转体的表面积为 .
绕直线SE 转一周所得到的旋转体的表面积为 .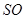 的侧面积为
的侧面积为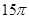 ,底面半径
,底面半径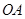 和
和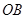 互相垂直,且
互相垂直,且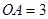 ,
,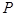 是母线
是母线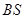 的中点.
的中点.
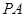 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).