题目内容
多面体ABCDEF的直观图及三视图分别如图所示,已知点M在AC上,点N在DE上,且AM∶MC=DN∶NE=a.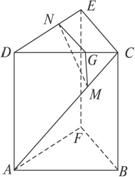
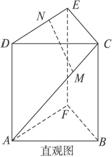
(1)求证:MN∥平面BCEF;
(2)当a=1时,求二面角D—MN—F的余弦值的绝对值.
解:(1)由三视图可知,该多面体是底面为直角三角形的直三棱柱ABF—DCE.
且AB=BC=AF=2,CE=BF=2![]() ,∠BAF=90°,
,∠BAF=90°,

在CD上取一点G,DG∶GC=DN∶NE,连结MG,NG.则
∵AM∶MC=DN∶NE=a,
∴NG∥CE,MG∥BC.
∴平面MNG∥平面BCEF.
∴MN∥平面BCEF.
(2)∵a=1,
∴M,N分别是AC、DE的中点.
以AB,AF,AD分别为x轴,y轴,z轴,建立空间直角坐标系,则有关各点的坐标分别是D(0,0,2),F(0,2,0),M(1,0,1),N(0,1,2)
∴![]() =(0,1,0),
=(0,1,0),![]() =(-1,1,1),
=(-1,1,1),![]() =(0,-1,2).
=(0,-1,2).
设平面DMN的法向量m=(1,y,z),则![]() ·m=0,
·m=0,![]() ·m=0.
·m=0.
∴![]()
∴![]()
∴m=(1,0,1).
设平面MNF的法向量为n=(1,y1,z1),则![]() ·n=0,
·n=0,![]() ·n=0.
·n=0.
∴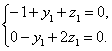
∴n=(1,![]() ,
,![]() ).
).
设二面角D—MN—F的平面角为θ,
则cosθ=![]() .
.
∴二面角D—MN—F的余弦值的绝对值为![]() .
.

练习册系列答案
相关题目
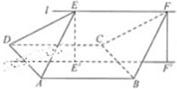 如图,ABCD的边长为2的正方形,直线l与平面ABCD平行,E和F是l上的两个不同点,且EA=ED,FB=FC,E′和F′是平面ABCD内的两点,E′E和F′F都与平面ABCD垂直,
如图,ABCD的边长为2的正方形,直线l与平面ABCD平行,E和F是l上的两个不同点,且EA=ED,FB=FC,E′和F′是平面ABCD内的两点,E′E和F′F都与平面ABCD垂直, 如图,ABCD是边长为3正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°. 如图正方形ABCD和四边形ADEF所在的平面垂直,FA⊥AD,DE∥FA,且
如图正方形ABCD和四边形ADEF所在的平面垂直,FA⊥AD,DE∥FA,且 如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.
如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.