Question

如图，已知ABCD是边长为2的正方形，DE⊥平面ABCD，BF⊥平面ABCD，且FB=2DE=2．
（1）求证：平面AEC⊥平面AFC；
（2）求多面体ABCDEF的体积．

Answer 1

分析：（1）以D为坐标原点，DA，DC，DE分别为X，Y，Z轴正言论自由建立空间直角坐标系，分别求出各点坐标，进而求出平面AEC和平面AFC的法向量的坐标，代入向量夹角公式，根据两个法向量的数量积为0，即可得到平面AEC⊥平面AFC；
（2）根据面面平行的性质定理，BC即为平面ABFE上的高，求出△AEF的面积，并将其代入棱锥体积公式，即可得到答案．

解答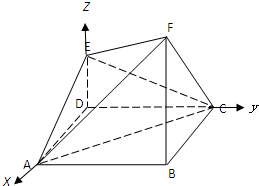：解：（1）证明：建立如图坐标系
∴D（0，0，0），E（0，0，1），A（2，0，0），C（0，2，0），F（2，2，2）
∴

AE

=(-2，0，1)，

EC

=(0，2，-1)

AF

=(0，2，2)，

FC

=(-2，0，-2)
设

m

为面AEC法向量 

m

=(x1，y1，z1)

-2x1+z1=0 2y1-z1=0

⇒

m

=(1，1，2)
设

n

为面AFC法向量 

n

=(x2，y2，z2)

2y2+2z2=0 -2x2-2z2=0

⇒

n

=(1，1，-1)cos＜

m

•

n

＞=

1+1-2

4 • 3

=0∴

m

⊥

n

．
∴面AEC⊥面AFC．
（2）S_△AEF=

1

2

•AE•EF=

1

2

∵平面ABEF⊥平面ABCD
即BC⊥AB
而平面ABEF∩平面ABCD=AB
∴BC⊥平面ABFE
∴V_C-AEF=

1

3

•S_△AEF•BC=

1

6

点评：本题考查的知识点是棱锥的体积公式，用向量语言表述面面垂直关系，其中（1）中用向量法证明面面垂直的关键是建立适当的空间直角坐标法，（2）中求棱锥的体积，确定底面和高是关键．