题目内容
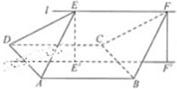 如图,ABCD的边长为2的正方形,直线l与平面ABCD平行,E和F是l上的两个不同点,且EA=ED,FB=FC,E′和F′是平面ABCD内的两点,E′E和F′F都与平面ABCD垂直,
如图,ABCD的边长为2的正方形,直线l与平面ABCD平行,E和F是l上的两个不同点,且EA=ED,FB=FC,E′和F′是平面ABCD内的两点,E′E和F′F都与平面ABCD垂直,(1)证明:直线E′F′垂直且平分线段AD:
(2)若∠EAD=∠EAB=60°,EF=2,求多面体ABCDEF的体积.
分析:(1)根据EA=ED且EE'⊥平面ABCD证出E'D=E'C,则点E'在线段AD的垂直平分线上,同理证出F'在线段BC的垂直平分线上,再由ABCD是正方形证出结论;
(2)根据图形连接EB、EC,由题意证出BE=FC=2,则多面体ABCD可分割成正四棱锥E-ABCD和正四面体E-BCF,根据条件求出这两个几何体的体积,求VE-BCF需要换低求出.
(2)根据图形连接EB、EC,由题意证出BE=FC=2,则多面体ABCD可分割成正四棱锥E-ABCD和正四面体E-BCF,根据条件求出这两个几何体的体积,求VE-BCF需要换低求出.
解答: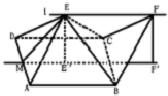 解:(1)∵EA=ED且EE'⊥平面ABCD,∴E'D=E'C,
解:(1)∵EA=ED且EE'⊥平面ABCD,∴E'D=E'C,
∴点E'在线段AD的垂直平分线上,同理点F'在线段BC的垂直平分线上.
又∵ABCD是正方形,
∴线段BC的垂直平分线也就是线段AD的垂直平分线
即点E′F′都居线段AD的垂直平分线上,
∴直线E′F′垂直平分线段AD.
(2)连接EB、EC,设AD中点为M,
由题意知,,AB=2,∠EAD=∠EAB=60°,EF=2,∴ME=
,BE=FC=2,
则多面体ABCD可分割成正四棱锥E-ABCD和正四面体E-BCF两部分,
在Rt△MEE 中,由于ME'=1,ME=
,∴EE'=
,
∴VE-ABCD=
S正方形ABCD•EE'=
×4×
=
,
∵VE-BCF=VC-BEF=VC-BEA=VE-ABC
=
S△ABC•EE'=
×
×4
=
,
∴多面体ABCDEF的体积为VE-BCF+VE-ABCD=2
.
 解:(1)∵EA=ED且EE'⊥平面ABCD,∴E'D=E'C,
解:(1)∵EA=ED且EE'⊥平面ABCD,∴E'D=E'C,∴点E'在线段AD的垂直平分线上,同理点F'在线段BC的垂直平分线上.
又∵ABCD是正方形,
∴线段BC的垂直平分线也就是线段AD的垂直平分线
即点E′F′都居线段AD的垂直平分线上,
∴直线E′F′垂直平分线段AD.
(2)连接EB、EC,设AD中点为M,
由题意知,,AB=2,∠EAD=∠EAB=60°,EF=2,∴ME=
| 3 |
则多面体ABCD可分割成正四棱锥E-ABCD和正四面体E-BCF两部分,
在Rt△MEE 中,由于ME'=1,ME=
| 3 |
| 2 |
∴VE-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
4
| ||
| 3 |
∵VE-BCF=VC-BEF=VC-BEA=VE-ABC
=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 2 |
∴多面体ABCDEF的体积为VE-BCF+VE-ABCD=2
| 2 |
点评:本题是关于线面垂直与组合体体积的求法综合题,利用线面垂直和线段相等证明垂直平分;用分割法可求得多面体体积,体现的是一种部分与整体的基本思想,求三棱锥的体积时常用换低来求解,考查了推理论证和逻辑思维能力.

练习册系列答案
相关题目
 已知:如图正方形ABCD的边长为a,P,Q分别为AB,DA上的点,当△PAQ的周长为2a时,求∠PCQ.
已知:如图正方形ABCD的边长为a,P,Q分别为AB,DA上的点,当△PAQ的周长为2a时,求∠PCQ.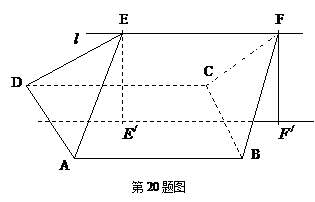 如图,ABCD的边长为2的正方形,直线
如图,ABCD的边长为2的正方形,直线