题目内容
【题目】某校从参加高三化学得分训练的学生中随机抽出60名学生,将其化学成绩(均为整数)分成六段![]() 、
、![]() 、…、
、…、![]() 后得到部分频率分布直方图(如图).
后得到部分频率分布直方图(如图).
观察图形中的信息,回答下列问题:
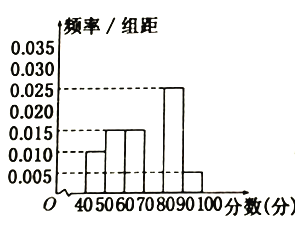
(1)求分数在![]() 内的频率,并补全频率分布直方图;
内的频率,并补全频率分布直方图;
(2)据此估计本次考试的平均分;
(3)若从60名学生中随机抽取2人,抽到的学生成绩在![]() 内记0分,在
内记0分,在![]() 内记1分,在
内记1分,在![]() 内记2分,用
内记2分,用![]() 表示抽取结束后的总记分,求
表示抽取结束后的总记分,求![]() 的分布列.
的分布列.
【答案】(1)答案见解析;(2)71;(3)答案见解析.
【解析】试题分析:
(1)利用频率分布直方图小长方形面积和为1列方程可得分数在![]() 内的频率是0.3,据此补全频率分布直方图即可;
内的频率是0.3,据此补全频率分布直方图即可;
(2)由频率分布直方图可估计平均分为71;
(3)由题意可得![]() 的可能取值是0,1,2,3,4,利用超几何分布的概率公式求得相应的概率值即可得到其分布列.
的可能取值是0,1,2,3,4,利用超几何分布的概率公式求得相应的概率值即可得到其分布列.
试题解析:
(1)设分数在![]() 内的频率为
内的频率为![]() ,根据频率分布直方图,有
,根据频率分布直方图,有![]() ,可得
,可得![]() .
.
(2)平均分为![]() .
.
(3)成绩在![]() 内的有
内的有![]() 人,在
人,在![]() 内的有
内的有![]() 人,在
人,在![]() 内的有
内的有![]() 人,易知
人,易知![]() 的可能取值是0,1,2,3,4,
的可能取值是0,1,2,3,4,
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|

 名校课堂系列答案
名校课堂系列答案【题目】某城市理论预测2007年到2011年人口总数与年份的关系如表所示
年份2007+x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请根据表提供的数据,求最小二乘法求出y关于x的线性回归方程;
(2)据此估计2012年该城市人口总数.
参考公式: 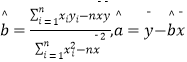 .
.
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机抽调了50人,他们年龄的频数分布及支持“生育二胎”人数如下表:
年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
(1)由以上统计数据填下面2×2列联表;
年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
支持“生育二胎” | a= | c= | |
不支持“生育二胎” | b= | d= | |
合计 |
(2)判断是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
附表:K2= ![]() .
.
