题目内容
【题目】已知复数集合![]()
![]() ,其中
,其中![]() 为虚数单位,若复数
为虚数单位,若复数![]() ,则
,则![]() 对应的点
对应的点![]() 在复平面内所形成图形的面积为________
在复平面内所形成图形的面积为________
【答案】![]()
【解析】
先由复数的几何意义确定集合![]() 所对应的平面区域,再确定集合
所对应的平面区域,再确定集合![]() 所对应的平面区域,由复数
所对应的平面区域,由复数![]() ,可得复数
,可得复数![]() 对应的点
对应的点![]() 在复平面内所形成图形即为集合
在复平面内所形成图形即为集合![]() 与集合
与集合![]() 所对应区域的重叠部分,结合图像求出面积即可.
所对应区域的重叠部分,结合图像求出面积即可.
因为复数集合![]() ,所以集合
,所以集合![]() 所对应的平面区域为
所对应的平面区域为![]() 与
与![]() 所围成的正方形区域;
所围成的正方形区域;
又![]() ,设
,设![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,
所以![]() ,设
,设![]() 对应的点为
对应的点为![]() ,
,
则 ,所以
,所以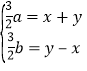 ,又
,又![]() ,
,![]() ,所以
,所以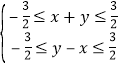 ,
,
因为复数![]() ,
,![]() 对应的点
对应的点![]() 在复平面内所形成图形即为集合
在复平面内所形成图形即为集合![]() 与集合
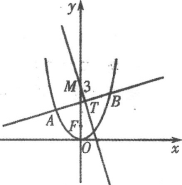
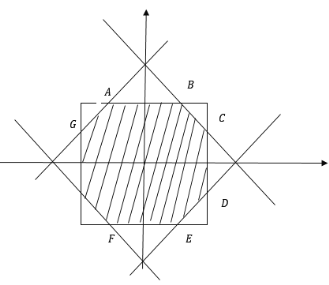
与集合![]() 所对应区域的重叠部分,如图中阴影部分所示,
所对应区域的重叠部分,如图中阴影部分所示,
由题意及图像易知:阴影部分为正八边形,只需用集合![]() 所对应的正方形区域的面积减去四个小三角形的面积即可.
所对应的正方形区域的面积减去四个小三角形的面积即可.
由 得
得![]() ,由
,由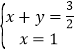 得
得![]() ,
,
所以![]() .
.
故答案为![]()

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目