题目内容
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是梯形,且
是梯形,且![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 的中点,过
的中点,过![]() 的平面
的平面![]() 交平面
交平面![]() 于
于![]() ,且
,且![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)先证明四边形![]() 是平行四边形,可得
是平行四边形,可得![]() ,则可证明
,则可证明![]() 平面
平面![]() ,再利用线面平行的性质定理证明
,再利用线面平行的性质定理证明![]() ;
;
(2)先证明![]() ,
,![]() ,
,![]() 两两垂直,则可建立如图所示的空间直角坐标系
两两垂直,则可建立如图所示的空间直角坐标系![]() ,求出
,求出![]() ,再求出平面
,再求出平面![]() 的一个法向量,可得直线
的一个法向量,可得直线![]() 与平面
与平面![]() 所成角的正弦值,进一步求解余弦值.
所成角的正弦值,进一步求解余弦值.
(1)证明:因为![]() 且
且![]() ,所以四边形
,所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
所以![]() ;
;
(2)在![]() 中,因为
中,因为![]() ,
,![]() ,
,
所以由正弦定理![]() ,即
,即![]() ,
,
所以![]() ,∴
,∴![]() ,∴在
,∴在![]() 中
中![]()
所以![]() ,
,
因为![]() 是等腰三角形,且
是等腰三角形,且![]() ,点
,点![]() 是线段
是线段![]() 的中点,
的中点,
得![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() 为
为![]() 中点,所以
中点,所以![]() ,
,
又由已知![]() 且
且![]() ,故
,故![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ;
;
在![]() 中,由
中,由![]() ,
,![]() ,可知
,可知![]() ,
,
易知四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,
故![]() ,
,![]() ,
,![]() 两两垂直;
两两垂直;
所以建立如图所示的空间直角坐标系![]() ,
,
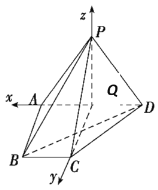
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
又![]() ,
,![]() ,所以
,所以 ,
,
即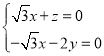 ,令
,令![]() ,解得
,解得![]() ,
,![]() ,
,
所以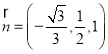 为平面
为平面![]() 的一个法向量,
的一个法向量,
因为![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则 ,
,
∴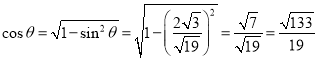 ,
,
故直线![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某公司甲、乙两个班组分别试生产同一种规格的产品,已知此种产品的质量指标检测分数不小于70时,该产品为合格品,否则为次品,现随机抽取两个班组生产的此种产品各100件进行检测,其结果如下表:
质量指标检测分数 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
甲班组生产的产品件数 | 7 | 18 | 40 | 29 | 6 |
乙班组生产的产品件数 | 8 | 12 | 40 | 32 | 8 |
(1)根据表中数据,估计甲、乙两个班组生产该种产品各自的不合格率;
(2)根据以上数据,完成下面的2×2列联表,并判断是否有95%的把握认为该种产品的质量与生产产品的班组有关?
甲班组 | 乙班组 | 合计 | |
合格品 | |||
次品 | |||
合计 |
(3)若按合格与不合格比例,从甲班组生产的产品中抽取4件产品,从乙班组生产的产品中抽取5件产品,记事件A:从上面4件甲班组生产的产品中随机抽取2件,且都是合格品;事件B:从上面5件乙班组生产的产品中随机抽取2件,一件是合格品,一件是次品,试估计这两个事件哪一种情况发生的可能性大.
附:![]()
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
【题目】已知表1和表2是某年部分日期的天安门广场升旗时刻表.
表1:某年部分日期的天安门广场升旗时刻表
日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 |
1月1日 | 7:36 | 4月9日 | 5:46 | 7月9日 | 4:53 | 10月8日 | 6:17 |
1月21日 | 7:31 | 4月28日 | 5:19 | 7月27日 | 5:07 | 10月26日 | 6:36 |
2月10日 | 7:14 | 5月16日 | 4:59 | 8月14日 | 5:24 | 11月13日 | 6:56 |
3月2日 | 6:47 | 6月3日 | 4:47 | 9月2日 | 5:42 | 12月1日 | 7:16 |
3月22日 | 6:15 | 6月22日 | 4:46 | 9月20日 | 5:59 | 12月20日 | 7:31 |
表2:某年2月部分日期的天安门广场升旗时刻表
日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 |
2月1日 | 7:23 | 2月11日 | 7:13 | 2月21日 | 6:59 |
2月3日 | 7:22 | 2月13日 | 7:11 | 2月23日 | 6:57 |
2月5日 | 7:20 | 2月15日 | 7:08 | 2月25日 | 6:55 |
2月7日 | 7:17 | 2月17日 | 7:05 | 2月27日 | 6:52 |
2月9日 | 7:15/p> | 2月19日 | 7:02 | 2月28日 | 6:49 |
(1)从表1的日期中随机选出一天,试估计这一天的升旗时刻早于7:00的概率;
(2)甲,乙二人各自从表2的日期中随机选择一天观看升旗,且两人的选择相互独立.记![]() 为这两人中观看升旗的时刻早于7:00的人数,求
为这两人中观看升旗的时刻早于7:00的人数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(3)将表1和表2中的升旗时刻化为分数后作为样本数据(如7:31化为![]() ).记表2中所有升旗时刻对应数据的方差为
).记表2中所有升旗时刻对应数据的方差为![]() ,表1和表2中所有升旗时刻对应数据的方差为
,表1和表2中所有升旗时刻对应数据的方差为![]() ,判断
,判断![]() 与
与![]() 的大小(只需写出结论)
的大小(只需写出结论)
【题目】“开门大吉”是某电视台推出的游戏节目,选手面对1![]() 号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金,在一次场外调查中,发现参赛选手多数分为两个年龄段:
号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金,在一次场外调查中,发现参赛选手多数分为两个年龄段: ![]() ;
; ![]() (单位:岁),其猜对歌曲名称与否的人数如图所示.
(单位:岁),其猜对歌曲名称与否的人数如图所示.

(Ⅰ)写出![]() 列联表;判断是否有
列联表;判断是否有![]() 的把握认为猜对歌曲名称是否与年龄有关;说明你的理由;(如表的临界值表供参考)
的把握认为猜对歌曲名称是否与年龄有关;说明你的理由;(如表的临界值表供参考)
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
(Ⅱ)现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手,并抽取3名幸运选手,求3名幸运选手中恰好有一人在![]() 岁之间的概率.
岁之间的概率.
(参考公式:  ,其中
,其中![]() )
)

