题目内容
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)令![]() ,是否存在实数
,是否存在实数![]() ,使得当
,使得当![]() 时,函数
时,函数![]() 的最小值是3?若存在,求出实数
的最小值是3?若存在,求出实数![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)当![]() 时,证明
时,证明![]() .
.
【答案】(1)![]() (2)存在,
(2)存在,![]() (3)见解析
(3)见解析
【解析】
(1)先求导可得![]() ,则可将问题转化为
,则可将问题转化为![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,设
上恒成立,设![]() ,求得
,求得![]() ,即可求解;
,即可求解;
(2)先对![]() 求导,再分别讨论
求导,再分别讨论![]() ,
,![]() ,
,![]() 时的情况,由最小值为3,进而求解;
时的情况,由最小值为3,进而求解;
(3)令![]() ,结合(2)中知
,结合(2)中知![]() 的最小值为3.再令
的最小值为3.再令![]() 并求导,再由导函数在
并求导,再由导函数在![]() 大于等于0可判断出函数
大于等于0可判断出函数![]() 在
在![]() 上单调递增,从而可求得最大值也为3,即有
上单调递增,从而可求得最大值也为3,即有![]() 成,,即
成,,即![]() 成立,即可得证.
成立,即可得证.
(1)解:![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上恒成立,
上恒成立,
设![]() ,则
,则![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]()
所以![]()
(2)解:存在,
假设存在实数![]() ,使
,使![]() 有最小值3,
有最小值3,
![]()
①当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,解得
,解得![]() (舍去);
(舍去);
②当![]() 时,当
时,当![]() ,则
,则![]() ;当
;当![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() ,解得
,解得![]() ,满足条件;
,满足条件;
③当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,解得
,解得![]() (舍去),
(舍去),
综上,存在实数![]() ,使得当
,使得当![]() 时
时![]() 有最小值3.
有最小值3.
(3)证明:令![]() ,由(2)知,
,由(2)知,![]() ,
,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
∴![]()
∴![]() ,
,
即![]() .
.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
【题目】支付宝和微信支付已经成为现如今最流行的电子支付方式,某市通过随机询问100名居民(男女居民各50名)喜欢支付宝支付还是微信支付,得到如下的![]() 列联表:
列联表:
支付宝支付 | 微信支付 | |
男 | 40 | 10 |
女 | 25 | 25 |
附表及公式: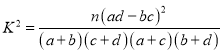 ,
,![]() .
.
P( | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
则下面结论正确的是( )
A.有![]() 以上的把握认为“支付方式与性别有关”
以上的把握认为“支付方式与性别有关”
B.在犯错误的概率超过![]() 的前提下,认为“支付方式与性别有关”
的前提下,认为“支付方式与性别有关”
C.在犯错误的概率不超过![]() 的前提下,认为“支付方式与性别有关”
的前提下,认为“支付方式与性别有关”
D.有![]() 以上的把握认为“支付方式与性别无关”
以上的把握认为“支付方式与性别无关”