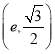题目内容
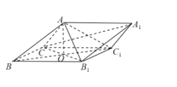
【题目】如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为∠CBB1=60°的菱形,AB=AC1 .

(1)证明:平面AB1C⊥平面BB1C1C
(2)若AB⊥B1C,直线AB与平面BB1C1C所成的角为30°,求直线AB1与平面A1B1C 所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)推导出![]() ,
,![]() ,从而
,从而![]() ⊥平面
⊥平面![]() ,由此能证明平面
,由此能证明平面![]() ⊥平面
⊥平面![]() ;(2)以
;(2)以![]() 为原点建立空间直角坐标系,由直线
为原点建立空间直角坐标系,由直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,得
,得![]() ,设
,设![]() ,利用向量法能求出直线
,利用向量法能求出直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
证明:(1)连接![]() 交
交![]() 于O,连接AO,侧面
于O,连接AO,侧面![]() 为菱形,
为菱形,
∴![]() ,
,![]() ,0为
,0为![]() 的中点,
的中点,
∴![]() 又
又![]() ,
,![]() ⊥平面
⊥平面![]() ,
,![]() 平面
平面![]()
∴平面![]() ⊥平面
⊥平面![]()
(2)由![]() ,
,![]() ,
,![]() ,∴
,∴![]() ⊥平面ABO,
⊥平面ABO,![]() 平面ABO, ∴
平面ABO, ∴![]() 从而AO,OB,
从而AO,OB,![]() 两两互相垂直,以O为坐标原点,OB的方向为x轴正方向,建立如图所示空间直角坐标系O-xyz,直线AB与平面
两两互相垂直,以O为坐标原点,OB的方向为x轴正方向,建立如图所示空间直角坐标系O-xyz,直线AB与平面![]() 所成的角为30°。
所成的角为30°。

设AO=1,则![]() ,又
,又![]() ,
,![]() 是边长为2的等边三角形
是边长为2的等边三角形
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]()
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则
令![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
则![]() ,
,![]()
直线与平面所成角的正弦值为![]() .
.

练习册系列答案
相关题目