题目内容
设f(x)是R上的奇函数,且f(x+2)=-f(x),当0≤x≤1时,f(x)=x,则f(75)等于( )
| A.-0 5 | B.0 5 | C. 1 5 | D.-1 5 |
A
分析:题目中条件:“f(x+2)=-f(x),”可得f(x+4)=f(x),故f(7.5)=f(-0.5)=-f(0.5)=-0.5.
解答:解:∵f(x+2)=-f(x),∴可得f(x+4)=f(x),
∵f(x)是(-∞,+∞)上的奇函数
∴f(-x)=-f(x).
∴故f(7.5)=f(-0.5)=-f(0.5)=-0.5.
故选A.
解答:解:∵f(x+2)=-f(x),∴可得f(x+4)=f(x),
∵f(x)是(-∞,+∞)上的奇函数
∴f(-x)=-f(x).
∴故f(7.5)=f(-0.5)=-f(0.5)=-0.5.
故选A.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
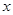 )=
)=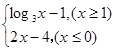 的反函数是
的反函数是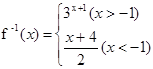

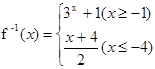
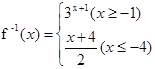
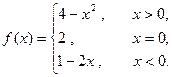
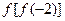 的值;
的值;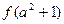 (
(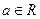 )的值;
)的值;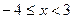 时,求函数
时,求函数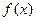 的值域。
的值域。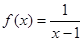 ,则函数
,则函数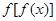 的定义域是( )
的定义域是( )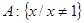
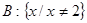
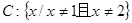

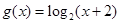
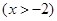
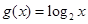
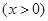
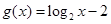
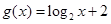

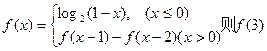 =
= 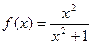 的值域为 .
的值域为 .