题目内容
已知函数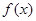
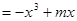 在
在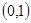 上是增函数
上是增函数
(1)求实数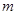 的取值集合
的取值集合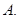
(2)当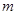 取值集合
取值集合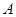 中的最小值时, 定义数列
中的最小值时, 定义数列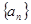 ;满足
;满足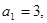 且
且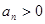 ,
, 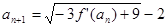 , 设
, 设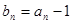 , 证明:数列
, 证明:数列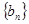 是等比数列, 并求数列
是等比数列, 并求数列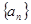 的通项公式.
的通项公式.
(3)若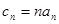 , 数列
, 数列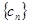 的前
的前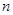 项和为
项和为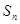 , 求
, 求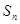 .
.
(1)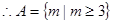 (2)
(2)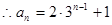 (3)
(3)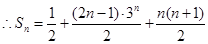
解析试题分析:(1)因为函数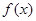 在
在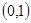 上是增函数, 只需
上是增函数, 只需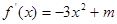 在
在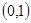 满足
满足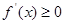 恒成立, 即
恒成立, 即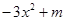
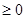
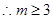
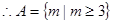 4分
4分
(2)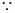
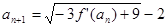 ,
, 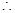
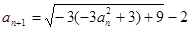
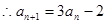
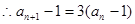
即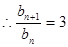 ,
, 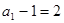
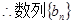 是等比数列, 首项为
是等比数列, 首项为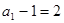 , 公比为3
, 公比为3 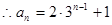 8分
8分
(3)由(2)可知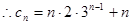
令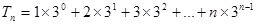 ,
, 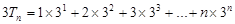
两式相减得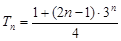
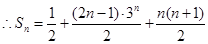 12分
12分
考点:函数单调性,数列求通项求和
点评:第一问由单调性可转化为导数的取值范围,第二问是通过构造新数列转化为等差或等比数列,第三问求和时数列通项是关于n的一次函数式与指数式的形式,这样的数列一般采用错位相减法求和

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
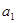 =2,点(
=2,点(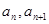 )在函数
)在函数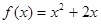 的图像上,其中
的图像上,其中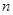 =
=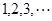 .
.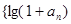 }是等比数列;
}是等比数列;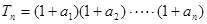 ,求
,求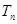 及数列{
及数列{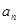 }的通项公式;
}的通项公式;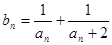 ,求数列{
,求数列{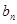 }的前n项和
}的前n项和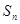 ,并证明
,并证明 .
.  的前项和为
的前项和为 ,满足
,满足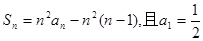 ,
,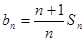 ,证明:
,证明: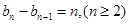 ;
;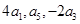 成等差数列.
成等差数列. 对任意
对任意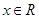 都有
都有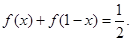
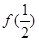 和
和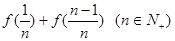 的值.
的值. 满足:
满足: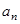 =
=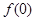 +
+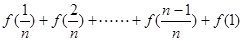 ,数列
,数列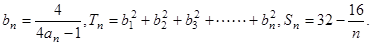 试比较
试比较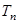 与
与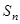 的大小.
的大小. ,求n的值;
,求n的值; 的数学公式表示上述结论,并给予证明。
的数学公式表示上述结论,并给予证明。
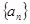 中,
中,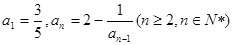 ,数列
,数列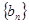 满足
满足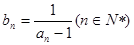 。
。