题目内容
(2010•潍坊三模)已知函数f(x)=
x2+2x(a∈R),g(x)=lnx.
(1)若函数h(x)=g(x)-f(x)存在单调递减区间,求a的取值范围;
(2)当a=l时,证明:x=1是函数y=f'(x)-
-2的唯一极值点.
分析:(1)先求函数h(x)的导函数h′(x),再将函数存在单调递减区间问题转化为导函数h′(x)<0在(0,+∞)上有解问题,最后参变分离将此问题转化为求函数最值问题即可得a的取值范围
(2)先求出函数y=f'(x)-
-2的解析式,即y=x-
,求其导函数y′,证明x=1是函数y′=
的零点,再由单调性证明y′=0有唯一根x=1,最后由函数y=f'(x)-
-2的单调性,证明x=1是函数y=f'(x)-
-2的极值点,从而证明x=1是函数y=f'(x)-
-2的唯一极值点
解答:解:(1)h(x)=lnx-
x2-2x (x>0),则h′(x)=
-ax-2
若函数h(x)=g(x)-f(x)存在单调递减区间,则h′(x)=
-ax-2<0在(0,+∞)上有解
而当x>0时,
-ax-2<0?ax>
-2?a>
-
问题转化为a>
-
在(0,+∞)上有解
∵
-
=
(-1)2-1≥-1,即
-
在(0,+∞)上的值域为[-1,+∞)
∴a>-1
(2)当a=1时,f(x)=
x
2+2x,∴y=x-
,
函数y′=1-
=
∵x=1时,y′=0,∴x=1是函数y′的零点
令M(x)=x
2+lnx-1,则x=1是M(x)=0的根
下面证明M(x)=0无其它根
M′(x)=2x+
,当x>0时,M′(x)>0,即y=M(x)在(0,+∞)上是单调增函数
∴M(x)=0有唯一根x=1
下面证明x=1是函数y=f'(x)-
-2的极值点
当x∈(0,1)时,y′=
<0,
∴y=f'(x)-
-2在(0,1)上是减函数
x∈(1,+∞)时,y′=
>0,
∴y=f'(x)-
-2在(0,1)上是增函数
∴x=1是函数y=f'(x)-
-2的极值点.
综上所述,x=1是函数y=f'(x)-
-2的唯一极值点
点评:本题考查了导数在函数单调性和极值问题中的应用,将函数性质与不等式的根的分布、零点存在性及唯一性互相转化的能力,推理证明的能力
练习册系列答案
相关题目

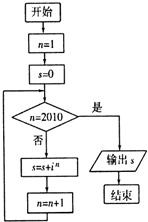 (2010•潍坊三模)运行如图所示的程序框图输出的结果是(其中i是虚数单位)( )
(2010•潍坊三模)运行如图所示的程序框图输出的结果是(其中i是虚数单位)( )