题目内容
数列{an}的前n项和记为Sn,前kn项和记为Skn(n,k∈N*),对给定的常数k,若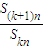 是与n无关的非零常数t=f(k),则称该数列{an}是“k类和科比数列”.
是与n无关的非零常数t=f(k),则称该数列{an}是“k类和科比数列”.(1)已知
 ,求数列{an}的通项公式;
,求数列{an}的通项公式;(2)在(1)的条件下,数列
 ,求证数列cn是一个“1 类和科比数列”(4分);
,求证数列cn是一个“1 类和科比数列”(4分);(3)设等差数列{bn}是一个“k类和科比数列”,其中首项b1,公差D,探究b1与D的数量关系,并写出相应的常数t=f(k).
【答案】分析:(1)利用an=Sn-Sn-1可以推导出数列an为等比数列,然后将a1=2,q=4代入等比数列的通项公式即可求出数列{an}的通项公式;
(2)根据(1)中求出的an的通项公式便可求出cn的通项公式为cn=2n-1,然后求出 为定值,便可证明数列cn是一个“1 类和科比数列”;
为定值,便可证明数列cn是一个“1 类和科比数列”;
(3)根据题中“k类和科比数列”的定义,将 =t便可求出D与b1的关系,继而可以求出常数t的表达式.
=t便可求出D与b1的关系,继而可以求出常数t的表达式.
解答:解:(1)联立: ,
,
∴ ,
,
∴ ,
,
所以{an}是等比数列,
由 ,得 a1=2,
,得 a1=2,
故 an=2•4n-1 =22n-1 .
(2)cn=2n-1前n项的和Sn=n2(1分)
S2n=4n2 , ,
,
所以数列{an}是一个“1类和科比数列”.
(3)对任意一个等差数列数列bn,首项b1,公差D,
 .
.
 ,
,
 ,对一切n∈N*恒成立,
,对一切n∈N*恒成立,
2(k+1)b1+(k+1)((k+1)n-1)=2ktb1+k(kn-1)Dt对一切n∈N*恒成立,
(k+1-kt)(2b1-D)=n•D(k2t-(k+1)2)对一切n∈N*恒成立,
所以 ,
,
D=2b1 ,
所以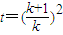 .
.
点评:本题考查了等差数列的基本性质以及数列的递推公式,考查了学生的计算能力和对数列的综合掌握,解题时注意整体思想和转化思想的运用,属于中档题.
(2)根据(1)中求出的an的通项公式便可求出cn的通项公式为cn=2n-1,然后求出
 为定值,便可证明数列cn是一个“1 类和科比数列”;
为定值,便可证明数列cn是一个“1 类和科比数列”;(3)根据题中“k类和科比数列”的定义,将
 =t便可求出D与b1的关系,继而可以求出常数t的表达式.
=t便可求出D与b1的关系,继而可以求出常数t的表达式.解答:解:(1)联立:
 ,
,∴
 ,
,∴
 ,
,所以{an}是等比数列,
由
 ,得 a1=2,
,得 a1=2,故 an=2•4n-1 =22n-1 .
(2)cn=2n-1前n项的和Sn=n2(1分)
S2n=4n2 ,
 ,
,所以数列{an}是一个“1类和科比数列”.
(3)对任意一个等差数列数列bn,首项b1,公差D,
 .
. ,
, ,对一切n∈N*恒成立,
,对一切n∈N*恒成立,2(k+1)b1+(k+1)((k+1)n-1)=2ktb1+k(kn-1)Dt对一切n∈N*恒成立,
(k+1-kt)(2b1-D)=n•D(k2t-(k+1)2)对一切n∈N*恒成立,
所以
 ,
,D=2b1 ,
所以
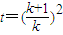 .
.点评:本题考查了等差数列的基本性质以及数列的递推公式,考查了学生的计算能力和对数列的综合掌握,解题时注意整体思想和转化思想的运用,属于中档题.

练习册系列答案
相关题目