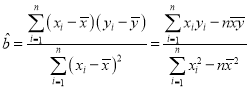题目内容
【题目】某人经营淡水池塘养草鱼,根据过去![]() 期的养殖档案,该池塘的养殖重量
期的养殖档案,该池塘的养殖重量![]() (百斤)都在
(百斤)都在![]() 百斤以上,其中不足
百斤以上,其中不足![]() 百斤的有
百斤的有![]() 期,不低于
期,不低于![]() 百斤且不超过
百斤且不超过![]() 百斤的有
百斤的有![]() 期,超过
期,超过![]() 百斤的有
百斤的有![]() 期.根据统计,该池塘的草鱼重量的增加量
期.根据统计,该池塘的草鱼重量的增加量![]() (百斤)与使用某种饵料的质量
(百斤)与使用某种饵料的质量![]() (百斤)之间的关系如图所示.
(百斤)之间的关系如图所示.
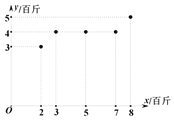
(1)根据数据可知![]() 与
与![]() 具有线性相关关系,请建立
具有线性相关关系,请建立![]() 关于
关于![]() 的回归方程
的回归方程![]() ;如果此人设想使用某种饵料
;如果此人设想使用某种饵料![]() 百斤时,草鱼重量的增加量须多于
百斤时,草鱼重量的增加量须多于![]() 百斤,请根据回归方程计算,确定此方案是否可行?并说明理由.
百斤,请根据回归方程计算,确定此方案是否可行?并说明理由.
(2)养鱼的池塘对水质含氧量与新鲜度要求较高,某商家为该养殖户提供收费服务,即提供不超过![]() 台增氧冲水机,每期养殖使用的冲水机运行台数与鱼塘的鱼重量
台增氧冲水机,每期养殖使用的冲水机运行台数与鱼塘的鱼重量![]() 有如下关系:
有如下关系:
鱼的重量(单位:百斤) |
|
|
|
冲水机只需运行台数 |
|
|
|
若某台增氧冲水机运行,则商家每期可获利![]() 千元;若某台冲水机未运行,则商家每期亏损
千元;若某台冲水机未运行,则商家每期亏损![]() 千元.视频率为概率,商家欲使每期冲水机总利润的均值达到最大,应提供几台增氧冲水机?
千元.视频率为概率,商家欲使每期冲水机总利润的均值达到最大,应提供几台增氧冲水机?
附:对于一组数据![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为
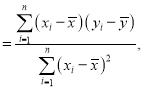
![]()
【答案】(1)![]() 当
当![]() 时,此方案可行.(2)应提供
时,此方案可行.(2)应提供![]() 台增氧冲水机
台增氧冲水机
【解析】
(1)求出,![]() .代入公式得到回归方程.代入
.代入公式得到回归方程.代入![]() ,求出估计值再进行判断.
,求出估计值再进行判断.
(2)分三个方案分别计算盈利的期望,选择期望高者即可.
解:(1)依题意,![]()
![]()
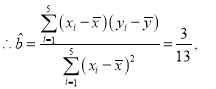
![]()
所以![]()
当![]() 时,
时,![]() ,故此方案可行.
,故此方案可行.
(2)设盈利为![]() ,
,
安装![]() 台时,盈利
台时,盈利![]() ,
,
安装![]() 台时,
台时,![]() ;
;
![]() .
.
![]()
安装![]() 台时,
台时,![]() ;
;
![]()
![]()
![]() .
.
![]()
![]() .
.
![]() ,故应提供
,故应提供![]() 台增氧冲水机.
台增氧冲水机.

练习册系列答案
相关题目