题目内容
已知数列{an}满足a1＝2，an＋1＝
(n∈N*)，则a3＝________，a1·a2·a3·…·a2007＝________．
(n∈N*)，则a3＝________，a1·a2·a3·…·a2007＝________．－
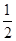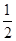，3
，3(解法1)分别求出a2＝－3、a3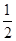＝－、a4＝
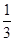、a5＝2，可以发现a5＝a1，且a1·a2·a3·a4＝1，故a1·a2·a3·…·a2 007＝a2 005·a2 006·a2 007＝a1·a2·a3＝3.
(解法2)由an＋1＝，联想到两角和的正切公式，设a1＝2＝tanθ，则有a2＝tan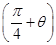
，a3＝tan
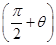，a4＝tan
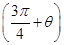，a5＝tan(π＋θ)＝a1，….则a1·a2·a3·a4＝1，
故a1·a2·a3·…·a2 007＝a2 005·a2 006·a2 007＝a1·a2·a3＝3.
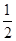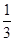、a4＝、a5＝2，可以发现a5＝a1，且a1·a2·a3·a4＝1，故a1·a2·a3·…·a2 007＝a2 005·a2 006·a2 007＝a1·a2·a3＝3.(解法2)由an＋1＝
，联想到两角和的正切公式，设a1＝2＝tanθ，则有a2＝tan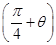，a3＝tan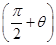，a4＝tan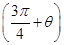，a5＝tan(π＋θ)＝a1，….则a1·a2·a3·a4＝1，故a1·a2·a3·…·a2 007＝a2 005·a2 006·a2 007＝a1·a2·a3＝3.
练习册系列答案
名校课堂系列答案
相关题目
，则三角形的面积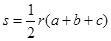
，根据类比思想，若四面体内切球半径为R，四个面的面积为S1、S2、S3、S4，则四面体的体积V= .
.将这个结论类比到空间：在三棱锥A－BCD中，平面DEC平分二面角A－CD－B且与AB交于E，则类比的结论为
＝________．
行的从左至右的第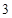
个数是 .
”类比可得“若三棱锥表面积为S，体积为V，则其内切球半径r＝
”；
”类比可得“若三棱锥三条侧棱两两垂直，侧棱长分别为a、b、c，则其外接球半径r＝
”．这两位同学类比得出的结论( )
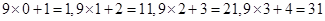，……，猜想第
（
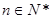）个等式应为_ _.
.
.
.
.
”，
的一次因式的积的形式）