题目内容
如图所示是某水产养殖厂的养殖大网箱的平面图,四周的实线为网衣,为避免混养,
(1)若大网箱的面积为108平方米,每个小网箱的横边 、纵边
、纵边 设计为多少米时,才能使围成的网箱中筛网的总长度最小?
设计为多少米时,才能使围成的网箱中筛网的总长度最小?
(2)若大网箱的面积为160平方米,网衣的造价为112元/米,筛网的造价为96元/米,且大网箱的长与宽都不超过15米,则小网箱的横、纵边分别为多少米时,可使总造价最低?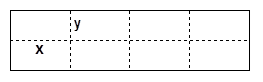
(1)若大网箱的面积为108平方米,每个小网箱的横边
 、纵边
、纵边 设计为多少米时,才能使围成的网箱中筛网的总长度最小?
设计为多少米时,才能使围成的网箱中筛网的总长度最小?(2)若大网箱的面积为160平方米,网衣的造价为112元/米,筛网的造价为96元/米,且大网箱的长与宽都不超过15米,则小网箱的横、纵边分别为多少米时,可使总造价最低?

(1)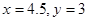 时总长度最小(2)当
时总长度最小(2)当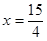 ,
,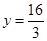 时总造价最低
时总造价最低
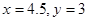 时总长度最小(2)当
时总长度最小(2)当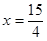 ,
,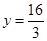 时总造价最低
时总造价最低试题分析:(1)问题为:
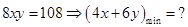
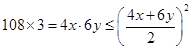
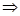
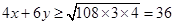
当
 时取等号.
时取等号.(2)问题为:
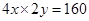 ,且
,且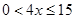 ,
,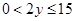
求
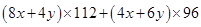 的最小值.
的最小值.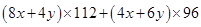 =
= =
=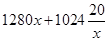 =
=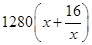

由
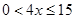 ,
,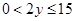
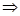
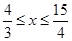 ,所以当
,所以当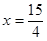 时总造价最低,此时
时总造价最低,此时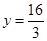 .
.点评:首先将应用中的实际问题转化为数学问题求最值,第一问利用了均值不等式求得的最值,第二问均值不等式等号成立的条件不满足,因此结合函数图象及单调性求得最值

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
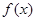 为定义在
为定义在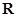 上的奇函数,当
上的奇函数,当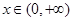 时,
时,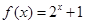 ,则当
,则当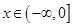 时,
时,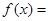 _______________.
_______________.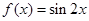 的图像向左平移
的图像向左平移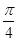 个单位,所得图像的解析式是( )
个单位,所得图像的解析式是( )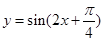
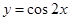
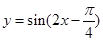
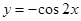
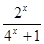 .
.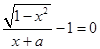 仅有一解,则实数
仅有一解,则实数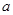 的取值范围是 .
的取值范围是 .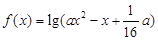 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式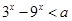 对任意
对任意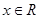 恒成立.
恒成立.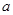 的取值范围;
的取值范围;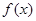 的定义域为A,若
的定义域为A,若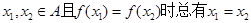 则称
则称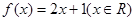 是单函数.下列命题:
是单函数.下列命题: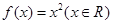 是单函数;
是单函数;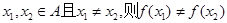 ;
;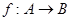 为单函数,则对于任意b
为单函数,则对于任意b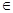 B,它至多有一个原象;
B,它至多有一个原象;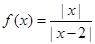 是偶函数;
是偶函数;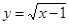 的值域为
的值域为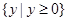 ;
;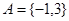 ,
,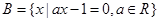 ,若
,若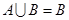 ,则
,则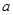 的取值集合为
的取值集合为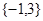 ;
;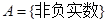 ,
,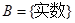 ,对应法则
,对应法则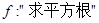 ,则
,则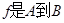 的映射;
的映射;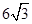 m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.