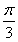Question

已知x0，x0＋是函数f(x)＝cos2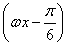－sin2ωx(ω＞0)的两个相邻的零点．

(1)求f的值；

(2)若对?x∈，都有|f(x)－m|≤1，求实数m的取值范围．

 

Answer 1

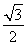（1）（2）

【解析】(1)f(x)＝＝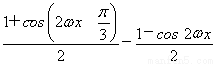

＝＝

＝＝.

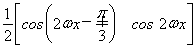
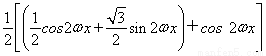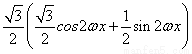由题意可知，f(x)的最小正周期T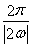＝π，∴＝π，

又∵ω＞0，∴ω＝1，∴f(x)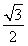＝ sin.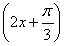

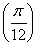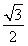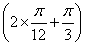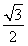∴f＝ sin＝ sin＝.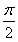

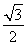(2)|f(x)－m|≤1，即f(x)－1≤m≤f(x)＋1，

∵对?x∈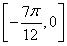，都有|f(x)－m|≤1，∴m≥f(x)max－1且m≤f(x)min＋1，

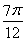∵－≤x≤0，∴－≤2x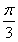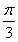＋≤，∴－1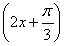≤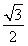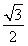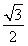sin≤，

∴－≤sin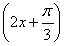≤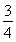，即f(x)max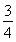＝，f(x)min＝－，

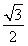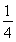∴－≤m≤1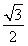－.故m的取值范围为