题目内容
2.设数列{an}满足:a1=$\sqrt{3}$,an+1=[an]+$\frac{1}{\{{a}_{n}\}}$,其中,[an]、{an}分别表示正数an的整数部分、小数部分,则a2016=3023+$\frac{\sqrt{3}-1}{2}$.分析 由已知求出数列的前几项,得到数列的项呈现的规律得答案.
解答 解:∵an+1=[an]+$\frac{1}{\{{a}_{n}\}}$,且a1=$\sqrt{3}$=1+($\sqrt{3}-1$),
∴${a}_{2}=[{a}_{1}]+\frac{1}{\{{a}_{1}\}}=1+\frac{1}{\sqrt{3}-1}=1+\frac{\sqrt{3}+1}{2}$=$2+\frac{\sqrt{3}-1}{2}$,
${a}_{3}=[{a}_{2}]+\frac{1}{\{{a}_{2}\}}=2+\frac{1}{\frac{\sqrt{3}-1}{2}}=2+\frac{2}{\sqrt{3}-1}$=$4+(\sqrt{3}-1)$,
${a}_{4}=[{a}_{3}]+\frac{1}{\{{a}_{3}\}}=4+\frac{1}{\sqrt{3}-1}=4+\frac{\sqrt{3}+1}{2}$=$5+\frac{\sqrt{3}-1}{2}$,
${a}_{5}=[{a}_{4}]+\frac{1}{\{{a}_{4}\}}=5+\frac{1}{\frac{\sqrt{3}-1}{2}}=5+\frac{2}{\sqrt{3}-1}$=$7+(\sqrt{3}-1)$,
${a}_{6}=[{a}_{5}]+\frac{1}{\{{a}_{5}\}}=7+\frac{1}{\sqrt{3}-1}=7+\frac{\sqrt{3}+1}{2}=8+$$\frac{\sqrt{3}-1}{2}$,
${a}_{7}=[{a}_{6}]+\frac{1}{\{{a}_{6}\}}=8+\frac{2}{\sqrt{3}-1}=8+\sqrt{3}+1$=$10+\sqrt{3}-1$,
${a}_{8}=[{a}_{7}]+\frac{1}{\{{a}_{7}\}}=10+\frac{1}{\sqrt{3}-1}=10+\frac{\sqrt{3}+1}{2}$=$11+\frac{\sqrt{3}-1}{2}$.
…
∴a2016=2016+1007+$\frac{\sqrt{3}-1}{2}$=3023+$\frac{\sqrt{3}-1}{2}$.
故答案为:3023+$\frac{\sqrt{3}-1}{2}$.
点评 本题是新定义题,考查了数列递推式,关键是由数列前几项得到数列的规律,是中档题.

| A. | 正三角形 | B. | 等腰三角形 | C. | 不等边三角形 | D. | 等腰直角三角形 |
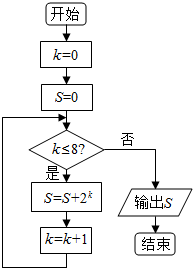
| A. | 1023 | B. | 512 | C. | 511 | D. | 255 |
 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,短轴的一个顶点与椭圆两焦点构成的三角形面积为2$\sqrt{3}$.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,短轴的一个顶点与椭圆两焦点构成的三角形面积为2$\sqrt{3}$.