题目内容
设F1、F2是双曲线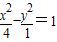 的两个焦点,点P在双曲线上,且
的两个焦点,点P在双曲线上,且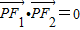 ,则
,则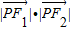 的值等于 .
的值等于 .
【答案】分析:依题意可知a2=4,b2=12,进而求得c,求得|F1F2|,令|PF1|=p,|PF2|=q,由勾股定理得p2+q2=|F1F2|2,求得p2+q2的值,由双曲线定义:|p-q|=2a两边平方,把p2+q2代入即可求得pq即|PF1|•|PF2|的值.
解答:解:依题意可知a2=4,b2=1
所以c2=5
∴|F1F2|=2c=2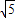
令|PF1|=p,|PF2|=q
由双曲线定义:|p-q|=2a=4
平方得:p2-2pq+q2=16
∵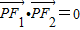 ,∴∠F1PF2=90°,由勾股定理得:
,∴∠F1PF2=90°,由勾股定理得:
p2+q2=|F1F2|2=20
所以pq=2
即|PF1|•|PF2|=2
故答案为:2.
点评:本题主要考查了双曲线的性质.要利用好双曲线的定义是解答的关键.
解答:解:依题意可知a2=4,b2=1
所以c2=5
∴|F1F2|=2c=2
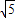
令|PF1|=p,|PF2|=q
由双曲线定义:|p-q|=2a=4
平方得:p2-2pq+q2=16
∵
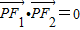 ,∴∠F1PF2=90°,由勾股定理得:
,∴∠F1PF2=90°,由勾股定理得:p2+q2=|F1F2|2=20
所以pq=2
即|PF1|•|PF2|=2
故答案为:2.
点评:本题主要考查了双曲线的性质.要利用好双曲线的定义是解答的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目