题目内容
将一枚硬币抛掷n次，求正面次数与反面次数之差ξ的概率分布，并求出ξ的期望Eξ与方差Dξ.
见解析
解：设正面的次数是η，由题意η服从二项分布B(n，0.5)，
概率分布为P(η=k)=
，k=0，l，……，n，
且Eξ=0.5n，Dξ=0.25n；而反面次数为n－η，从而ξ=η－(n－η)=2η－n,
于是，ξ的概率分布为 P(ξ=2η－n)＝P(η="k)="， k=0，1，……，n；
即P(ξ=k)=P(η=
)=
，k=－n，－n+2，－n+4，……，n
故Eξ=E(2η－n)=2Eξ－n=2×0.5n－n=0；Dξ=D(2η－n)=22Dξ=4×0.25n＝n
概率分布为P(η=k)=
，k=0，l，……，n，且Eξ=0.5n，Dξ=0.25n；而反面次数为n－η，从而ξ=η－(n－η)=2η－n,
于是，ξ的概率分布为 P(ξ=2η－n)＝P(η="k)="
， k=0，1，……，n；即P(ξ=k)=P(η=
)=，k=－n，－n+2，－n+4，……，n故Eξ=E(2η－n)=2Eξ－n=2×0.5n－n=0；Dξ=D(2η－n)=22Dξ=4×0.25n＝n
练习册系列答案
小学夺冠AB卷系列答案
相关题目
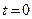时刻一质点在数轴的原点，该质点
每经过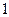
秒就要向右跳动一个单位长度，已知每次跳动，该质点向左的概率为
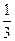，向右的概率为
．
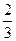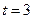秒时刻，该质点在数轴上
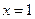处的概率．
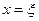处，求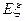
、
．
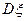
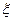，求随机变量
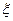；乙抛掷3次，记正面朝上的次为
.（Ⅰ）分别求