题目内容
(本小题满分14分)
已知椭圆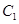 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为 ,
,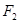
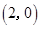 ,点
,点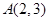 在椭圆
在椭圆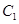 上,过点
上,过点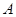 的直线
的直线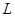 与抛物线
与抛物线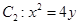 交于
交于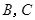 两点,抛物线
两点,抛物线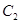 在点
在点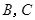 处的切线分别为
处的切线分别为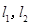 ,且
,且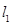 与
与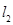 交于点
交于点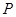 .
.
(1) 求椭圆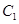 的方程;
的方程;
(2) 是否存在满足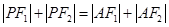 的点
的点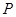 ? 若存在,指出这样的点
? 若存在,指出这样的点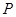 有几个(不必求出点
有几个(不必求出点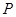 的坐标); 若不存在,说明理由.
的坐标); 若不存在,说明理由.
(1) 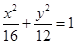 (2) 满足条件的点
(2) 满足条件的点 有两个
有两个
【解析】
试题分析:(1) 解法1:设椭圆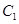 的方程为
的方程为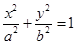
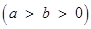 ,
,
依题意:  解得:
解得: 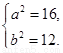
∴ 椭圆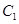 的方程为
的方程为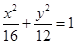 .
.
解法2:设椭圆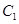 的方程为
的方程为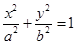
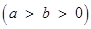 ,
,
根据椭圆的定义得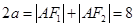 ,即
,即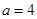 ,
,
∵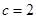 , ∴
, ∴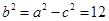 .
.
∴ 椭圆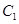 的方程为
的方程为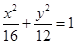 .
.
(2)解法1:设点 ,
,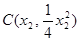 ,则
,则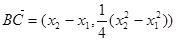 ,
,
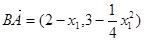 ,
,
∵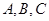 三点共线,
三点共线,
∴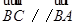 .
.
∴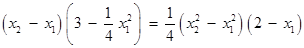 ,
,
化简得: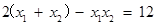 . ①
. ①
由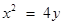 ,即
,即 得
得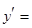
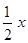 .
.
∴抛物线 在点
在点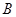 处的切线
处的切线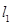 的方程为
的方程为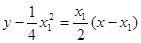 ,即
,即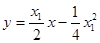 . ②
. ②
同理,抛物线 在点
在点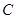 处的切线
处的切线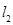 的方程为
的方程为  . ③
. ③
设点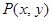 ,由②③得:
,由②③得: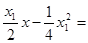
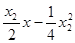 ,
,
而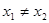 ,则
,则 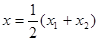 .
.
代入②得
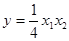 ,
,
则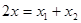 ,
,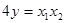 代入 ① 得
代入 ① 得
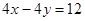 ,即点
,即点 的轨迹方程为
的轨迹方程为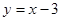 .
.
若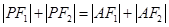 ,则点
,则点 在椭圆
在椭圆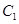 上,而点
上,而点 又在直线
又在直线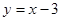 上,
上,
∵直线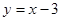 经过椭圆
经过椭圆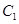 内一点
内一点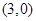 ,
,
∴直线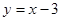 与椭圆
与椭圆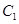 交于两点.
交于两点.
∴满足条件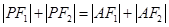 的点
的点 有两个.
有两个.
解法2:设点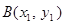 ,
,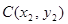 ,
,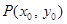 ,
,
由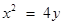 ,即
,即 得
得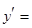
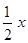 .
.
∴抛物线 在点
在点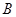 处的切线
处的切线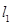 的方程为
的方程为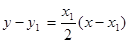 ,
,
即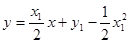 .
.
∵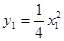 , ∴
, ∴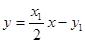 .
.
∵点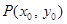 在切线
在切线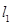 上, ∴
上, ∴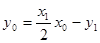 . ①
. ①
同理, 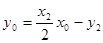 . ②
. ②
综合①、②得,点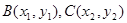 的坐标都满足方程
的坐标都满足方程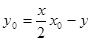 .
.
∵经过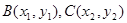 的直线是唯一的,
的直线是唯一的,
∴直线 的方程为
的方程为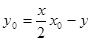 ,
,
∵点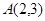 在直线
在直线 上, ∴
上, ∴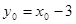 .
.
∴点 的轨迹方程为
的轨迹方程为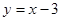 .
.
若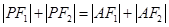 ,则点
,则点 在椭圆
在椭圆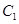 上,又在直线
上,又在直线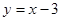 上,
上,
∵直线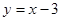 经过椭圆
经过椭圆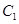 内一点
内一点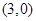 ,
,
∴直线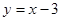 与椭圆
与椭圆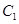 交于两点.
交于两点.
∴满足条件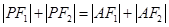 的点
的点 有两个.
有两个.
解法3:显然直线 的斜率存在,设直线
的斜率存在,设直线 的方程为
的方程为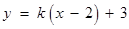 ,
,
由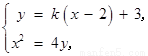 消去
消去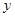 ,得
,得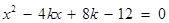 .
.
设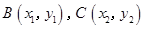 ,则
,则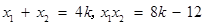 .
.
由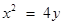 ,即
,即 得
得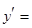
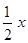 .
.
∴抛物线 在点
在点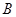 处的切线
处的切线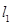 的方程为
的方程为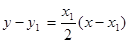 ,即
,即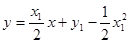 .
.
∵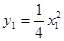 , ∴
, ∴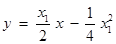 .
.
同理,得抛物线 在点
在点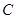 处的切线
处的切线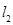 的方程为
的方程为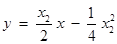 .
.
由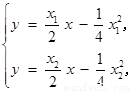 解得
解得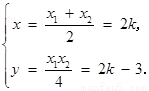
∴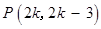 .
.
∵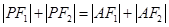 ,
,
∴点 在椭圆
在椭圆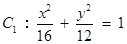 上.
上.
∴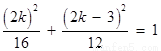 .
.
化简得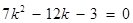 .(*)
.(*)
由 ,
,
可得方程(*)有两个不等的实数根. ∴满足条件的点 有两个.
有两个.
考点:椭圆抛物线方程及性质,直线与椭圆抛物线相交的应用
点评:求椭圆方程采用了待定系数法与定义法,其中待定系数法是常用的方法,而利用定义求解能使一些题目的计算量较小很多;第二问在直线与圆锥曲线相交的背景下常联立方程,利用韦达定理求解

 天天练口算系列答案
天天练口算系列答案 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)