题目内容
8.为了得到函数y=sin2x-$\sqrt{3}$cos2x的图象,只要把函数y=2sin2x的图象( )| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向左平移$\frac{π}{6}$个单位长度 | ||
| C. | 向右平移$\frac{π}{3}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
分析 由条件利用两角和差的正弦公式化简y=sin2x-$\sqrt{3}$cos2x的解析式,再利用函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:∵函数y=sin2x-$\sqrt{3}$cos2x=2sin(2x-$\frac{π}{3}$)=2sin2(x-$\frac{π}{6}$),
故把函数y=2sin2x的图象向右平移$\frac{π}{6}$个单位长度,即可得到函数y=sin2x-$\sqrt{3}$cos2x的图象,
故选:D.
点评 本题主要考查两角和差的正弦公式,函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知函数f(x)=lnx+x2-bx在其定义域内是增函数,则b的取值范围是( )
| A. | (-∞,2$\sqrt{2}$) | B. | (2$\sqrt{2}$,+∞) | C. | (-∞,2) | D. | (2,+∞) |
19.如图,在正方体ABCD-A1B1C1D1中,直线A1B与直线C1D1所成的角为( )
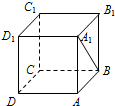

| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
16.在△ABC中,若a=3,c=$\sqrt{3},∠A=\frac{π}{3}$,则b=( )
| A. | 4 | B. | 6 | C. | $2\sqrt{3}$ | D. | $\sqrt{6}$ |
13.设i是虚数单位,则复数$\frac{1+2i}{i}$=( )
| A. | 2-i | B. | -2-i | C. | -2+i | D. | 2+i |
17.某电视台娱乐节目中,需要在编号分别为1、2、3、4、5的五个礼品盒中,装四个不同礼品,只有一个礼品盒是空盒.不同的装法有( )
| A. | 5种 | B. | 20种 | C. | 24种 | D. | 120种 |
 如图,在直角坐标系中,曲线段AB是函数y=1-x2图象的一部分,P为曲线段AB上异于点A,B一个动点,PM丄x轴,垂足为M,PN丄y轴,垂足为N.
如图,在直角坐标系中,曲线段AB是函数y=1-x2图象的一部分,P为曲线段AB上异于点A,B一个动点,PM丄x轴,垂足为M,PN丄y轴,垂足为N. 已知函数$f(x)=2sin(2x+\frac{π}{6})+1+a$,x∈[0,π]的最大值为2
已知函数$f(x)=2sin(2x+\frac{π}{6})+1+a$,x∈[0,π]的最大值为2