题目内容
15. 如图,四棱锥P-ABCD的底面ABCD是平行四边形,∠DAB=60°,AB=2AD=2,PD⊥平面ABCD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,∠DAB=60°,AB=2AD=2,PD⊥平面ABCD.(Ⅰ)求证:AD⊥PB;
(Ⅱ)若BD与平面PBC的所成角为30°,求二面角P-BC-D的余弦值.
分析 (Ⅰ)根据线面垂直的性质定理即可证明AD⊥PB.
(Ⅱ)建立空间直角坐标系,利用向量法即可求二面角P-BC-D的余弦值
解答 证明:(Ⅰ)因为∠DAB=60°,AB=2AD,
由余弦定理得BD2=AB2+AD2-2AB•ADcos∠DAB=3AD2,
从而BD2+AD2=AB2,
∴∠ADB=90°,故BD⊥AD,
又PD⊥底面ABCD,
可得PD⊥AD,
∴AD⊥平面PBD.
故AD⊥PB.
(Ⅱ)∵PD⊥底面ABCD,
∴PD⊥AD,PD⊥BD,
∵AD⊥BD,
∴以D为坐标原点,射线DA为x轴的正半轴建立空间直角坐标系D-xyz,
∵AB=2AD=2,∴AB=2,AD=1,
设DP=b,
则A(1,0,0),B(0,$\sqrt{3}$,0),C(-1,$\sqrt{3}$,0),P(0,0,b).
∴$\overrightarrow{DB}$=(0,$\sqrt{3}$,0),$\overrightarrow{BC}$=(-1,0,0),$\overrightarrow{PB}$=(0,$\sqrt{3}$,-b),
设$\overrightarrow{m}$=(x,y,z)是平面PBC的一个法向量,
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BD}=-x=0}\\{\overrightarrow{m}•\overrightarrow{PB}=\sqrt{3}y-bz=0}\end{array}\right.$,
令y=$\frac{\sqrt{3}}{3}$,则x=0,z=$\frac{1}{b}$,
则$\overrightarrow{m}$=(0,$\frac{\sqrt{3}}{3}$,$\frac{1}{b}$),
∵BD与平面PBC的所成角为30°,
∴$\overrightarrow{m}$与$\overrightarrow{DB}$的夹角为60°,
∴cos<$\overrightarrow{m}$,$\overrightarrow{DB}$>=$\frac{\overrightarrow{m}•\overrightarrow{DB}}{|\overrightarrow{m}||\overrightarrow{DB}|}$=$\frac{1}{\sqrt{\frac{1}{3}+(\frac{1}{b})^{2}}•\sqrt{3}}$=cos60°=$\frac{1}{2}$,
整理得b=1,
∴$\overrightarrow{m}$=(0,$\frac{\sqrt{3}}{3}$,1),
设$\overrightarrow{n}$=(x,y,z)是平面PAB的一个法向量,
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=-ax+\sqrt{3}ay=0}\\{\overrightarrow{n}•\overrightarrow{PB}=\sqrt{3}ay-az=0}\end{array}\right.$,
令y=$\frac{\sqrt{3}}{3}$,则x=1,z=1,
即$\overrightarrow{n}$=(1,$\frac{\sqrt{3}}{3}$,1)
∴cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overline{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{2\sqrt{7}}{7}$,
即二面角P-BC-D的余弦值是-$\frac{2\sqrt{7}}{7}$.
点评 本题主要考查空间线面垂直的性质,以及二面角的求解,利用向量法是解决二面角的常用方法.

| A. | 4n-1 | B. | 4n-1 | C. | 2n-1 | D. | 2n-1 |
| A. | $\sqrt{6}$+$\sqrt{3}$ | B. | $\frac{{\sqrt{6}+\sqrt{3}}}{2}$ | C. | $\sqrt{6}$+$\sqrt{2}$ | D. | $\frac{{\sqrt{6}+\sqrt{2}}}{2}$ |
| A. | p∧q | B. | (¬p)∨q | C. | (¬p)∧(¬q) | D. | p∧(¬q) |
 如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,AA1=$\sqrt{2}$a,E、F分别是AD、AB的中点.
如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,AA1=$\sqrt{2}$a,E、F分别是AD、AB的中点. 某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题: 如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记∠AOP为x(x∈[0,π]),OP所经过的在正方形ABCD内的区域(阴影部分)的面积S=f(x),那么对于函数f(x)有以下三个结论:
如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记∠AOP为x(x∈[0,π]),OP所经过的在正方形ABCD内的区域(阴影部分)的面积S=f(x),那么对于函数f(x)有以下三个结论: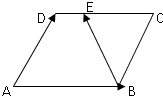 在边长为1的菱形ABCD中,∠A=60°,E是线段CD上一点,满足|$\overrightarrow{CE}$|=2||$\overrightarrow{DE}$|,如图所示,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
在边长为1的菱形ABCD中,∠A=60°,E是线段CD上一点,满足|$\overrightarrow{CE}$|=2||$\overrightarrow{DE}$|,如图所示,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.