题目内容
(本题满分12分)设函数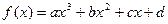 (a、b、c、d∈R)满足:
(a、b、c、d∈R)满足:
对任意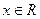 都有
都有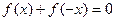 ,
,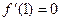 ,
,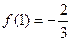
(1)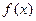 的解析式;
的解析式;
(2)当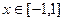 时,证明:函数图象上任意两点处的切线不可能互相垂直;
时,证明:函数图象上任意两点处的切线不可能互相垂直;
(3)设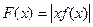 ,证明:
,证明: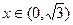 时,
时,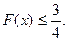
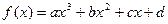 (a、b、c、d∈R)满足:
(a、b、c、d∈R)满足:对任意
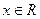 都有
都有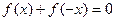 ,
,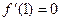 ,
,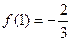
(1)
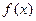 的解析式;
的解析式;(2)当
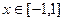 时,证明:函数图象上任意两点处的切线不可能互相垂直;
时,证明:函数图象上任意两点处的切线不可能互相垂直;(3)设
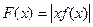 ,证明:
,证明: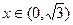 时,
时,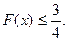
解:(I)因为,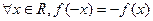 成立,所以:
成立,所以: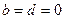 ,
,
由: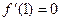 ,得
,得 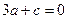 ,
,
由: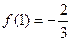 ,得
,得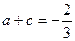
解之得: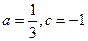 从而,函数解析式为:
从而,函数解析式为: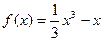 …………4分
…………4分
(2)由于,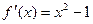 ,设:任意两数
,设:任意两数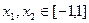 是函数
是函数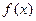 图像上两点的横坐
图像上两点的横坐
标,则这两点的切线的斜率分别是: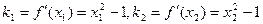
又因为: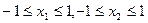 ,所以,
,所以, ,得:
,得: 知:
知: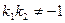
故,当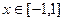 是函数
是函数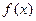 图像上任意两点的切线不可能垂直…………9分
图像上任意两点的切线不可能垂直…………9分
(3)当: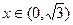 时,
时,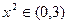 且
且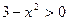 此时
此时

当且仅当: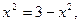 即
即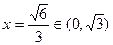 ,取等号,故:
,取等号,故: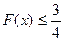 …………12分
…………12分
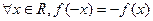 成立,所以:
成立,所以: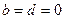 ,
,由:
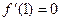 ,得
,得 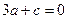 ,
,由:
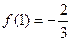 ,得
,得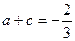
解之得:
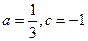 从而,函数解析式为:
从而,函数解析式为: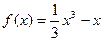 …………4分
…………4分(2)由于,
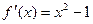 ,设:任意两数
,设:任意两数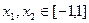 是函数
是函数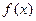 图像上两点的横坐
图像上两点的横坐标,则这两点的切线的斜率分别是:
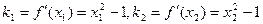
又因为:
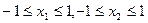 ,所以,
,所以, ,得:
,得: 知:
知: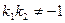
故,当
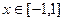 是函数
是函数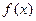 图像上任意两点的切线不可能垂直…………9分
图像上任意两点的切线不可能垂直…………9分(3)当:
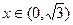 时,
时,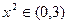 且
且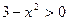 此时
此时
当且仅当:
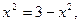 即
即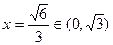 ,取等号,故:
,取等号,故: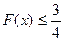 …………12分
…………12分略

练习册系列答案
相关题目
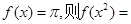 ( )
( ) B.
B.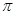 C.
C.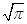 D.不确定
D.不确定
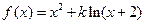 ,其中
,其中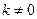
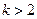 判断
判断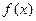 在
在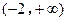 上的单调性.
上的单调性.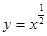 和函数
和函数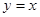 围成的图形的面积是( )
围成的图形的面积是( )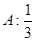
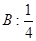
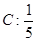

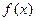 的图象经过点
的图象经过点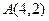 ,则它在
,则它在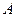 点处的切线方程为
点处的切线方程为  的导数
的导数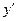 =__________________.
=__________________.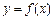 及其导函数
及其导函数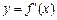 的图象如图所示,则曲线
的图象如图所示,则曲线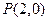 处的切线方程是
处的切线方程是 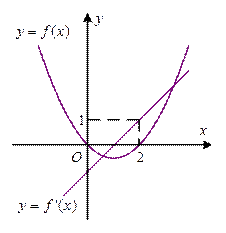
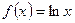 ,若直线
,若直线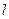 与
与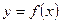 的图象相切的切点的横坐标为1,那么直线
的图象相切的切点的横坐标为1,那么直线
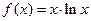 的单调递减区间是 .
的单调递减区间是 .