题目内容
7.在△ABC中,AC=3,∠A=$\frac{π}{4}$,点D满足$\overrightarrow{CD}$=2$\overrightarrow{DB}$,且AD=$\sqrt{13}$,则BC的长为3.分析 由已知,结合向量的基本运算可求得$\overrightarrow{AD}$=$\frac{1}{3}\overrightarrow{AC}+\frac{2}{3}\overrightarrow{AB}$,然后结合已知及向量数量积的定义及性质可求AB,最后利用余弦定理可求BC
解答 解:∵$\overrightarrow{CD}$=2$\overrightarrow{DB}$
∴$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}$=$\overrightarrow{AB}+\frac{1}{3}\overrightarrow{BC}$=$\overrightarrow{AB}+\frac{1}{3}(\overrightarrow{AC}-\overrightarrow{AB})$=$\frac{1}{3}\overrightarrow{AC}+\frac{2}{3}\overrightarrow{AB}$
∵AD=|$\overrightarrow{AD}$|=$\sqrt{13}$,AC=|$\overrightarrow{AC}$|=3,A=$\frac{π}{4}$,设AB=c
∴$\overrightarrow{AB}•\overrightarrow{AC}$=|$\overrightarrow{AB}$||$\overrightarrow{AC}$|cosA=$\frac{3\sqrt{2}}{2}c$
则13=$(\frac{1}{3}\overrightarrow{AC}+\frac{2}{3}\overrightarrow{AB})^{2}$=$\frac{1}{9}|\overrightarrow{AC}{|}^{2}+\frac{4}{9}|\overrightarrow{AB}{|}^{2}+\frac{4}{9}\overrightarrow{AB}•\overrightarrow{AC}$
∴13=1$+\frac{4{c}^{2}}{9}+\frac{2\sqrt{2}}{3}c$
整理可得,2c2$+3\sqrt{2}c$-54=0
∵c>0
解可得,c=3$\sqrt{2}$
由余弦定理可得,a2=c2+b2-2bc•cosA
=$(3\sqrt{2})^{2}+{3}^{2}-2×3×3\sqrt{2}×\frac{\sqrt{2}}{2}$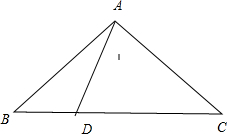
点评 本题主要考查了解三角形的简单应用,解题中要注意结合向量知识,要灵活的运用基本公式


| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
| A. | 1+i | B. | -1+i | C. | -1-i | D. | 1-i |
| A. | {x|x<0} | B. | {x|x<-1} | C. | {x|-1<x<0} | D. | {x|0<x<1} |
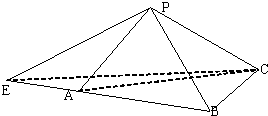 如图,在三棱锥P-ABC中,PA⊥平面PBC,PA=PB=2,PC=4,∠BPC=60°.
如图,在三棱锥P-ABC中,PA⊥平面PBC,PA=PB=2,PC=4,∠BPC=60°.