题目内容
如图,五面体中,四边形ABCD是矩形,DA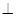 面ABEF,且DA=1,AB//EF,
面ABEF,且DA=1,AB//EF,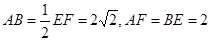 ,P、Q、M分别为AE、BD、EF的中点.
,P、Q、M分别为AE、BD、EF的中点.
求证:(I)PQ//平面BCE;
(II)求证:AM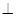 平面ADF;
平面ADF;
(I)见解析(II)见解析.
解析试题分析:(I)连接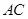 ,根据四边形ABCD是矩形,Q为BD的中点,推出Q为AC的中点,利用
,根据四边形ABCD是矩形,Q为BD的中点,推出Q为AC的中点,利用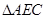 从而可得PQ//平面BCE.
从而可得PQ//平面BCE.
(II)由M是EF的中点,得到EM=AB=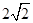 ,
,
推出四边形ABEM是平行四边形.
从而由AM//BE,AM=BE=2,AF=2,MF=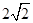 ,得到
,得到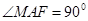 ,
,
推出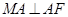 .又可得
.又可得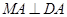 ,即可得出AM
,即可得出AM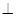 平面ADF.
平面ADF.
试题解析:(I)连接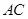 ,因为四边形ABCD是矩形,Q为BD的中点,所以,Q为AC的中点,
,因为四边形ABCD是矩形,Q为BD的中点,所以,Q为AC的中点,
又在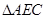 中,
中,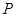 为
为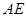 的中点,所以
的中点,所以 ,
,
因为,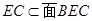 ,
,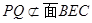 ,所以,PQ//平面BCE.
,所以,PQ//平面BCE.
(II)因为,M是EF的中点,所以,EM="AB=" 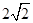 ,
,
又因为EF//AB,所以,四边形ABEM是平行四边形.
所以,AM//BE,AM=BE=2,
又AF=2,MF=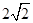 ,所以,
,所以,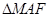 是直角三角形,且
是直角三角形,且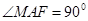 ,
,
所以,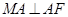 .
.
又因为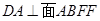 ,
, 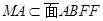 ,
,
所以,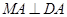 ,
,
又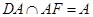 ,所以,AM
,所以,AM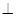 平面ADF.
平面ADF.
考点:平行关系,垂直关系.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
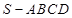 中,
中,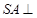 平面
平面 ,底面
,底面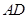 ∥
∥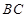 ,
,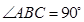 ,
,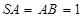 ,
,
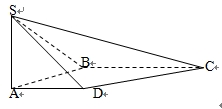
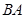 ⊥平面
⊥平面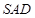 ;
;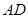 与
与 所成角的大小。
所成角的大小。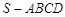 ,底面
,底面 为平行四边形,侧面
为平行四边形,侧面 底面
底面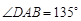 ,
, ,
,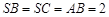 ,
,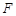 为线段
为线段 的中点.
的中点.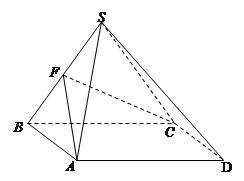
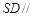 平面
平面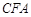 ;
; .
.
 中,
中, 平面
平面 ,
, 是正三角形,
是正三角形, 与
与 的交点
的交点 恰好是
恰好是 ,
, ,点
,点 在线段
在线段 上,且
上,且 .
.
 ;
; 平面
平面 ;
; 的余弦值.
的余弦值.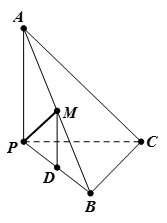
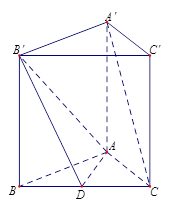
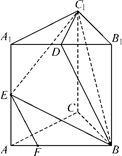
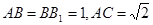 ,直线B1C与平面ABC成45°角。
,直线B1C与平面ABC成45°角。
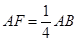
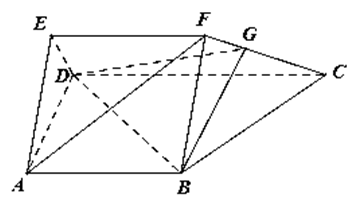
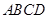 是梯形,
是梯形,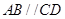 ,
,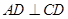 ,三角形
,三角形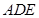 是等边三角形,且平面
是等边三角形,且平面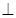 平面
平面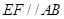 ,
,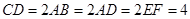 ,
,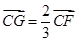
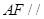 平面
平面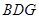 ;
;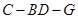 的余弦值.
的余弦值.