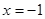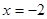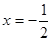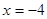题目内容
已知抛物线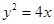 ,过焦点
,过焦点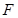 的直线交抛物线于
的直线交抛物线于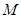 ,
,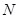 两点,以下命题:
两点,以下命题:
①若直线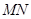 的倾斜角为
的倾斜角为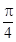 ,则
,则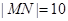 ;
;
②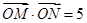 ;
;
③过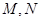 分别作准线
分别作准线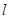 的垂线,垂足分别为
的垂线,垂足分别为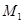 ,
,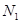 ,则
,则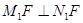 ;
;
④连接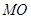 ,
,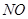 并延长分别交抛物线的准线于
并延长分别交抛物线的准线于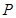 ,
,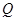 两点,则以
两点,则以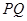 为直径的圆过焦点
为直径的圆过焦点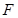
其中真命题的序号为 .
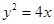 ,过焦点
,过焦点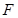 的直线交抛物线于
的直线交抛物线于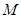 ,
,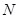 两点,以下命题:
两点,以下命题:①若直线
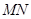 的倾斜角为
的倾斜角为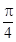 ,则
,则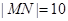 ;
;②
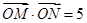 ;
;③过
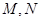 分别作准线
分别作准线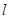 的垂线,垂足分别为
的垂线,垂足分别为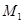 ,
,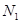 ,则
,则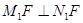 ;
;④连接
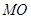 ,
,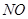 并延长分别交抛物线的准线于
并延长分别交抛物线的准线于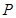 ,
,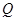 两点,则以
两点,则以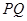 为直径的圆过焦点
为直径的圆过焦点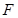
其中真命题的序号为 .
③④
依题意可得,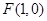 。当直线
。当直线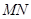 的倾斜角为
的倾斜角为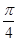 时,直线
时,直线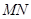 的方程为
的方程为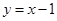 。联立
。联立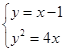 可得
可得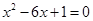 。设
。设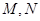 坐标分别为
坐标分别为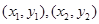 ,所以
,所以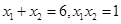 ,所以
,所以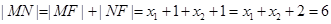 ,命题①不正确;
,命题①不正确;
当直线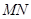 斜率不存在时,可得
斜率不存在时,可得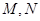 坐标为
坐标为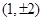 ,此时
,此时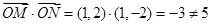 ;当直线
;当直线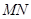 斜率存在时,设其方程为
斜率存在时,设其方程为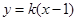 ,联立
,联立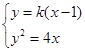 可得
可得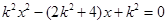 ,所以
,所以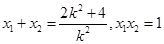 。因为
。因为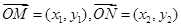 ,所以
,所以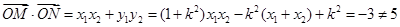 ,命题②不正确;
,命题②不正确;
依题意可得,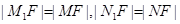 ,而
,而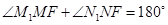 ,所以
,所以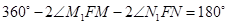 ,即
,即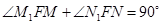 ,故
,故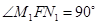 ,即
,即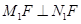 ,命题③正确;
,命题③正确;
依题意可得 ,则
,则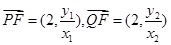 ,所以
,所以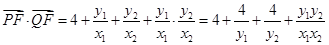 。当直线
。当直线 斜率不存在时,
斜率不存在时,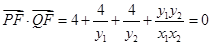 ;当直线
;当直线 斜率存在时,
斜率存在时,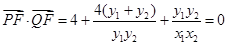 。综上可得,
。综上可得,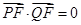 ,所以
,所以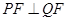 ,则以
,则以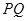 为直径的圆经过焦点
为直径的圆经过焦点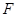 ,命题④正确。
,命题④正确。
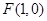 。当直线
。当直线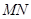 的倾斜角为
的倾斜角为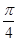 时,直线
时,直线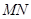 的方程为
的方程为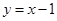 。联立
。联立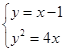 可得
可得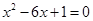 。设
。设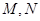 坐标分别为
坐标分别为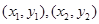 ,所以
,所以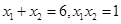 ,所以
,所以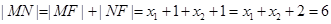 ,命题①不正确;
,命题①不正确;当直线
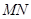 斜率不存在时,可得
斜率不存在时,可得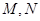 坐标为
坐标为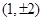 ,此时
,此时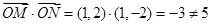 ;当直线
;当直线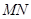 斜率存在时,设其方程为
斜率存在时,设其方程为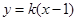 ,联立
,联立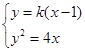 可得
可得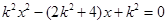 ,所以
,所以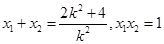 。因为
。因为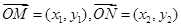 ,所以
,所以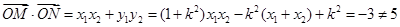 ,命题②不正确;
,命题②不正确;依题意可得,
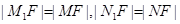 ,而
,而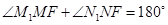 ,所以
,所以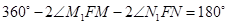 ,即
,即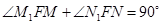 ,故
,故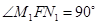 ,即
,即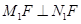 ,命题③正确;
,命题③正确;依题意可得
 ,则
,则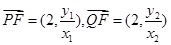 ,所以
,所以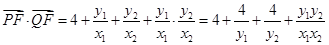 。当直线
。当直线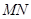 斜率不存在时,
斜率不存在时,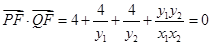 ;当直线
;当直线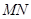 斜率存在时,
斜率存在时,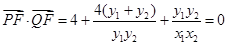 。综上可得,
。综上可得,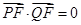 ,所以
,所以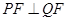 ,则以
,则以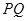 为直径的圆经过焦点
为直径的圆经过焦点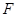 ,命题④正确。
,命题④正确。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
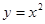 上到直线
上到直线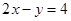 距离最近的点的坐标是______ ___.
距离最近的点的坐标是______ ___. 上一点到准线和抛物线的对称轴距离分别为10和6,则该点横坐标为
上一点到准线和抛物线的对称轴距离分别为10和6,则该点横坐标为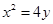 上与焦点的距离等于
上与焦点的距离等于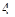 的点的纵坐标是 ( )
的点的纵坐标是 ( )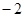 )的抛物线的标准方程为( )
)的抛物线的标准方程为( )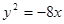
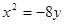
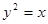 或
或
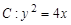 的焦点为
的焦点为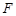 ,准线为
,准线为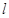 ,过抛物线
,过抛物线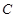 上的点
上的点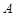 作准线
作准线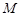 ,若
,若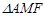 与
与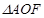 (其中
(其中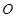 为坐标原点)的面积之比为
为坐标原点)的面积之比为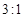 ,则点
,则点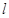 过抛物线
过抛物线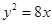 的焦点
的焦点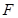 ,且与抛物线交于
,且与抛物线交于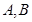 两点,若线段
两点,若线段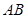 的中点到
的中点到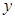 轴的距离是
轴的距离是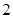 ,则
,则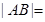 __ ▲ __.
__ ▲ __.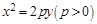 与直线
与直线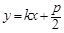 交于A、B两点,O为坐标原点.
交于A、B两点,O为坐标原点.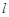 是该抛物线的准线.对于任意实数k,
是该抛物线的准线.对于任意实数k,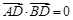 ?如果存在,求出点D的坐标;如不存在,说明理由.
?如果存在,求出点D的坐标;如不存在,说明理由. 
 ( )
( )