题目内容
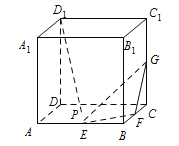
【题目】如图,在棱长为2的正方体![]() 中,
中,![]() 分别是棱
分别是棱![]() 的中点,
的中点,![]() 是底面
是底面![]() 内一动点,若直线
内一动点,若直线![]() 与平面
与平面![]() 不存在公共点,以下说法正确的个数是( )
不存在公共点,以下说法正确的个数是( )
①三棱锥![]() 的体积为定值;
的体积为定值;
②![]() 的面积的最小值为
的面积的最小值为![]() ;
;
③![]() 平面
平面![]() ;
;
④经过![]() 三点的截面把正方体分成体积相等的两部分.
三点的截面把正方体分成体积相等的两部分.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
由题意得,![]() 平面
平面![]() ,连接
,连接![]() ,则
,则![]() ,可得
,可得![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,由此得平面
,由此得平面![]() 平面
平面![]() ,则点
,则点![]() 在直线
在直线![]() 上,从而有
上,从而有![]() 的面积
的面积![]() 为定值,由此可判断①;结合题意得,当点
为定值,由此可判断①;结合题意得,当点![]() 为
为![]() 的交点时,
的交点时,![]() ,
,![]() 有最小值
有最小值![]() ,由此可判断②;由题意可得
,由此可判断②;由题意可得![]() 平面
平面![]() ,从而推出
,从而推出![]() ,
,![]() ,由此可判断③;将平面
,由此可判断③;将平面![]() 补成平面
补成平面![]() (
(![]() 均为各条棱的中点),结合图象可判断④.
均为各条棱的中点),结合图象可判断④.
解:∵直线![]() 与平面
与平面![]() 不存在公共点,
不存在公共点,
∴![]() 平面
平面![]() ,
,
连接![]() ,则
,则![]() ,
,
∵![]() 分别是棱
分别是棱![]() 的中点,
的中点,
∴![]() ,
,![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
同理,![]() 平面
平面![]() ,
,
又![]() ,
,
∴平面![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴点![]() 在直线
在直线![]() 上,
上,
∵![]() ,
,
∴![]() 的面积
的面积![]() 为定值,
为定值,
∴三棱锥![]() 的体积
的体积![]() 为定值,则①对;
为定值,则①对;
∵![]() ,
,
∴当点![]() 为
为![]() 的交点时,
的交点时,![]() ,
,![]() 有最小值
有最小值![]() ,
,
此时,直角![]() 的面积有最小值,且
的面积有最小值,且![]()
![]() ,则②对;
,则②对;
∵在正方体![]() 中,
中,![]() ,
,
由![]() 平面
平面![]() 得,
得,![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() ,则
,则![]() ,
,
同理,![]() ,
,
∴![]() 平面
平面![]() ,则③对;
,则③对;
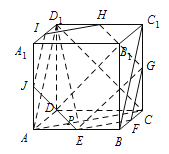
将平面![]() 补成平面
补成平面![]() (
(![]() 均为各条棱的中点),如图,
均为各条棱的中点),如图,
则平面![]() 将正方体分成两个大小形状完全相同的部分(均由一个正六棱锥和三个三棱锥拼接而成),则④对;
将正方体分成两个大小形状完全相同的部分(均由一个正六棱锥和三个三棱锥拼接而成),则④对;
故选:D.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目