题目内容
10．若曲线y=ax2+$\frac{b}{x}$（a，b为常数）过点P（2，-5），且该曲线在点P处的切线与直线7x+2y+3=0平行，则a+b的值为（ ）| A． | -5 | B． | 5 | C． | -3 | D． | 3 |
分析 求出函数的导数，求得切线的斜率，由直线平行的条件和切点的坐标可得a，b的方程，解方程可得a，b的和．
解答 解：y=ax2+$\frac{b}{x}$的导数为y′=2ax-$\frac{b}{{x}^{2}}$，
曲线在点P处的切线斜率为k=4a-$\frac{b}{4}$，
由两直线平行的条件可得4a-$\frac{b}{4}$=-$\frac{7}{2}$，
又4a+$\frac{b}{2}$=-5，
解得a=-1，b=-2．
即有a+b=-3．
故选C．
点评 本题考查导数的运用：求切线的斜率，考查导数的几何意义和两直线平行的条件，正确求导是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
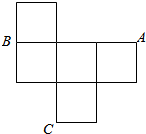如图是一个无盖的正方体盒子展开后的平面图，A，B，C展开图是上的三点，则在正方体盒子中，∠ABC=90°．