题目内容
已知命题p:方程a2x2+ax-2=0在[-1,1]上有解;命题q:只有一个实数x满足不等式x2+2ax+2a≤0,若命题“p或q”是假命题,求实数a的取值范围.
{a|-1<a<0或0<a<1}.
由a2x2+ax-2=0,得
(ax+2)(ax-1)=0,
显然a≠0,∴x=- 或x=
或x= .
.
∵x∈[-1,1],故 ≤1或
≤1或 ≤1,∴|a|≥1.
≤1,∴|a|≥1.
由题知命题q“只有一个实数x满足x2+2ax+2a≤0”,
即抛物线y=x2+2ax+2a与x轴只有一个交点,
∴Δ=4a2-8a=0,∴a=0或a=2,
∴当命题“p或q”为真命题时|a|≥1或a=0.
∵命题“p或q”为假命题,
∴a的取值范围为{a|-1<a<0或0<a<1}.
(ax+2)(ax-1)=0,
显然a≠0,∴x=-
 或x=
或x= .
.∵x∈[-1,1],故
 ≤1或
≤1或 ≤1,∴|a|≥1.
≤1,∴|a|≥1.由题知命题q“只有一个实数x满足x2+2ax+2a≤0”,
即抛物线y=x2+2ax+2a与x轴只有一个交点,
∴Δ=4a2-8a=0,∴a=0或a=2,
∴当命题“p或q”为真命题时|a|≥1或a=0.
∵命题“p或q”为假命题,
∴a的取值范围为{a|-1<a<0或0<a<1}.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 方程
方程 有两个不等的负实根;
有两个不等的负实根; 方程
方程 无实根.若
无实根.若 或
或 为真,
为真, 的取值范围.
的取值范围. ,则
,则 ”的否命题为:“若
”的否命题为:“若 ”
” ,则命题
,则命题
 ,则
,则 ”的逆否命题为真命题
”的逆否命题为真命题 ”是“
”是“ ”的必要不充分条件
”的必要不充分条件 -
- =1为双曲线,命题q:函数f(x)=(4-a)x在R上是增函数,且p∨q为真命题,p∧q为假命题,则实数a的取值范围是________.
=1为双曲线,命题q:函数f(x)=(4-a)x在R上是增函数,且p∨q为真命题,p∧q为假命题,则实数a的取值范围是________.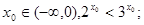 命题
命题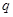 :“
:“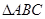 中,若
中,若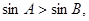 则
则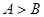 。则下列命题为真命题的是( )
。则下列命题为真命题的是( )




 ”是“
”是“ ”的充分不必要条件
”的充分不必要条件
 为假命题,则
为假命题,则 、
、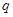 均为假命题
均为假命题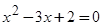 ,则
,则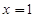 ”的逆否命题为“若
”的逆否命题为“若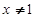 ,则
,则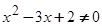 ”;
”;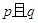 为假命题,则
为假命题,则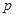 、
、 均为假命题.
均为假命题.