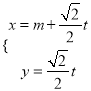Question

【题目】如图，已知OPQ是半径为1，圆心角为 的扇形，C是扇形弧上的动点，ABCD是扇形的内接矩形．记∠COP=α，则矩形ABCD的面积最大是 ．

Answer 1

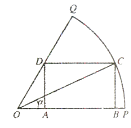
【答案】
【解析】解：如图，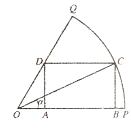
在Rt△OBC中，OB=cosα，BC=sinα，
在Rt△OAD中， =tan60°= ，
所以OA= DA= BC= sinα．
所以AB=OB﹣OA=cosα﹣ sinα．
设矩形ABCD的面积为S，
则S=ABBC=（cosα﹣ sinα）sinα=sinαcosα﹣ sin2α
= sin2α+ cos2α﹣ = （ sin2α+ cos2α）﹣
= sin（2α+ ）﹣ ．
由于0＜α＜ ，所以当2α+ = ，即α= 时，S最大= ﹣ = ．
因此，当α= 时，矩形ABCD的面积最大，最大面积为 ．
所以答案是： ．
【考点精析】本题主要考查了扇形面积公式的相关知识点，需要掌握若扇形的圆心角为，半径为，弧长为，周长为，面积为，则，，才能正确解答此题．