题目内容
【题目】已知函数  .
.
(1)请在直角坐标系中画出函数f(x)的图象,并写出该函数的单调区间;
(2)若函数g(x)=f(x)﹣m恰有3个不同零点,求实数m的取值范围.
【答案】
(1)解:f(x)= 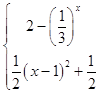 ,函数f(x)的图象如图所示:
,函数f(x)的图象如图所示:
由图象得:函数f(x)的单调递减区间是(0,1),单调增区间是(﹣∞,0),(1,+∞)
(2)解:作出直线y=m,函数g(x)=f(x)﹣m恰有3个不同零点等价于函数y=m与函数f(x)的图象恰有三个不同公共点.
由函数f(x)= 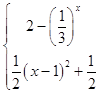 的图象易知:
的图象易知: ![]() .
.
故m的取值范围为( ![]() ,1).
,1).
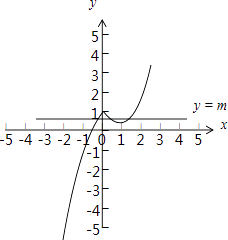
【解析】(1)x≤0的图象部分可由图象变换作出;x>0的部分为抛物线的一部分.(2)数形结合法:转化为直线y=m与函数f(x)的图象有三个交点.
【考点精析】认真审题,首先需要了解函数图象的作法(图象的作法与平移:①据函数表达式,列表、描点、连光滑曲线;②利用熟知函数的图象的平移、翻转、伸缩变换;③利用反函数的图象与对称性描绘函数图象),还要掌握函数的单调性(注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种)的相关知识才是答题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目