题目内容
3.设函数f(x)=(x-a)lnx-x+a,a∈R.(1)若a=0,求函数f(x)的单调区间;
(2)若a<0,试判断函数f(x)在区间(e-2,e2)内的极值点的个数,并说明理由;
(3)求证:对任意的正数a,都存在实数t,满足:对任意的x∈(t,t+a),f(x)<a-1.
分析 (1)求解f′(x)=lnx,利用f′(x)>0,f′(x)<0,解不等式求解单调递增区间,单调递减区间.
(2)f′(x)=lnx-$\frac{a}{x}$,其中x>0,
再次构造函数令g(x)=xlnx-a,分析g(x)的零点情况.g′(x)=lnx+1,
令g′(x)=0,x=$\frac{1}{e}$,列表分析得出g(x)单调性,判断g(x)min=g($\frac{1}{e}$)=-$\frac{1}{e}$-a,
分类讨论求解①若a≤-$\frac{1}{e}$,②若-$\frac{1}{e}$<a<-$\frac{2}{e2}$,③若-$\frac{2}{e2}$≤a<0,f(x)的单调性,f(x)最大值,最小值,
确定有无零点问题.
(3)先猜想x∈(1,1+a),f(x)<a-1恒成立.
再运用导数判断证明.令G(x)=lnx-x+1,x≥1.G′(x)=$\frac{1}{x}$-1≤0,求解最大值,
得出G(x)<G(1)=0即可.
解答 解:(1)当a=0时,f(x)=xlnx-x,f′(x)=lnx,
令f′(x)=0,x=1,列表分析
| x | (0,1) | 1 | (1,+∞) |
| f′(x) | - | 0 | + |
| f(x) | 单调递减 | 单调递增 |
(2)f(x)=(x-a)lnx-x+a,f′(x)=lnx-$\frac{a}{x}$,其中x>0,
令g(x)=xlnx-a,分析g(x)的零点情况.g′(x)=lnx+1,令g′(x)=0,x=$\frac{1}{e}$,列表分析
| x | (0,$\frac{1}{e}$) | $\frac{1}{e}$ | ($\frac{1}{e}$,+∞) |
| g′(x) | - | 0 | + |
| g(x) | 单调递减 | 单调递增 |
而f′($\frac{1}{e}$)=ln$\frac{1}{e}$-ae=-1-ae,f′(e-2)=-2-ae2=-(2+ae2),f′(e2)=2-$\frac{a}{e2}$=$\frac{1}{e2}$(2e2-a),
①若a≤-$\frac{1}{e}$,则f′(x)=lnx-$\frac{a}{x}$≥0,
故f(x)在(e-2,e2)内没有极值点;
②若-$\frac{1}{e}$<a<-$\frac{2}{e2}$,则f′($\frac{1}{e}$)=ln$\frac{1}{e}$-ae<0,f′(e-2)=-(2+ae2)>0,f′(e2)=$\frac{1}{e2}$(2e2-a)>0,
因此f′(x)在(e-2,e2)有两个零点,f(x)在(e-2,e2)内有两个极值点;
③若-$\frac{2}{e2}$≤a<0,则f′($\frac{1}{e}$)=ln$\frac{1}{e}$-ae<0,f′(e-2)=-(2+ae2)≤0,f′(e2)=$\frac{1}{e2}$(2e2-a)>0,
因此f′(x)在(e-2,e2)有一个零点,f(x)在(e-2,e2)内有一个极值点;
综上所述,当a∈(-∞,-$\frac{1}{e}$]时,f(x)在(e-2,e2)内没有极值点;
当a∈(-$\frac{1}{e}$,-$\frac{2}{e2}$)时,f(x)在(e-2,e2)内有两个极值点;
当a∈[-$\frac{2}{e2}$,0)时,f(x)在(e-2,e2)内有一个极值点.
(3)猜想:x∈(1,1+a),f(x)<a-1恒成立.
证明如下:
由(2)得g(x)在($\frac{1}{e}$,+∞)上单调递增,且g(1)=-a<0,g(1+a)=(1+a)ln(1+a)-a.
因为当x>1时,lnx>1-$\frac{1}{x}$(*),所以g(1+a)>(1+a)(1-$\frac{1}{a+1}$)-a=0.
故g(x)在(1,1+a)上存在唯一的零点,设为x0. 由
| x | (1,x0) | x0 | (x0,1+a) |
| f’(x) | - | 0 | + |
| f(x) | 单调递减 | 单调递增 |
又f(1+a)=ln(1+a)-1,而x>1时,lnx<x-1(**),
所以f(1+a)<(a+1)-1-1=a-1=f(1).
即x∈(1,1+a),f(x)<a-1.
所以对任意的正数a,都存在实数t=1,使对任意的x∈(t,t+a),使 f(x)<a-1.
补充证明(*):
令F(x)=lnx+$\frac{1}{x}$-1,x≥1.F′(x)=$\frac{1}{x}$-$\frac{1}{x2}$=$\frac{x-1}{x2}$≥0,
所以F(x)在[1,+∞)上单调递增.
所以x>1时,F(x)>F(1)=0,即lnx>1-$\frac{1}{x}$.
补充证明(**)
令G(x)=lnx-x+1,x≥1.G′(x)=$\frac{1}{x}$-1≤0,
所以G(x)在[1,+∞)上单调递减.
所以x>1时,G(x)<G(1)=0,即lnx<x-1.
点评 本题主要考查导数与函数单调性的关系,会熟练运用导数解决函数的极值与最值问题.求函数的单调区间,应该先求出函数的导函数,令导函数大于0得到函数的递增区间,令导函数小于0得到函数的递减区间,考查了不等式与导数的结合,难度较大.

练习册系列答案
相关题目
14.若△ABC所在平面内一点P使得$6\overrightarrow{PA}+3\overrightarrow{PB}+2\overrightarrow{PC}=\vec 0$,则△PAB,△PBC,△PAC的面积的比为( )
| A. | 6:3:2 | B. | 3:2:6 | C. | 2:6:3 | D. | 6:2:3 |
8.已知θ∈R,则“θ=$\frac{π}{6}$”是“cosθ=$\frac{\sqrt{3}}{2}$”的( )
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不必要也不充分条件 |
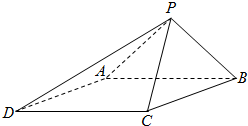 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.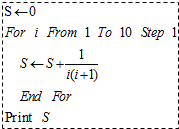
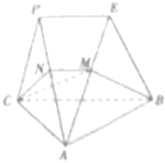 如图,平面PAC⊥平面ABC,AC⊥BC,△PAC是等边三角形,PE∥BC,过BC作平面CNMB交线段AP于点N,交线段AE于M.
如图,平面PAC⊥平面ABC,AC⊥BC,△PAC是等边三角形,PE∥BC,过BC作平面CNMB交线段AP于点N,交线段AE于M.