题目内容
18.已知0≤x≤2,求函数y=($\frac{1}{4}$)x-1-2•($\frac{1}{2}$)x+2的最大值和最小值.分析 换元用配方法求函数y=($\frac{1}{4}$)x-1-2•($\frac{1}{2}$)x+2的最大值和最小值.
解答 解:令($\frac{1}{2}$)x=t,则$\frac{1}{4}$≤t≤1,y=4t2-2t+2=4(t-$\frac{1}{4}$)2+$\frac{15}{8}$.
当t=$\frac{1}{4}$即x=2时,ymin=$\frac{15}{8}$;
当t=1即x=0时,ymax=2.
点评 本题考查了对数的运算性质以及值域,令($\frac{1}{2}$)x=t,则$\frac{1}{4}$≤t≤1,y=4t2-2t+2=4(t-$\frac{1}{4}$)2+$\frac{15}{8}$是解题的关键,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
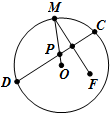 如图,圆心为O的圆形纸片内有一个定点F(点F与点O不重合),点M在圆周上,现把纸片折叠让点M与点F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,当点M在圆周上运动时,点P形成的轨迹是( )
如图,圆心为O的圆形纸片内有一个定点F(点F与点O不重合),点M在圆周上,现把纸片折叠让点M与点F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,当点M在圆周上运动时,点P形成的轨迹是( )